Feige’s Conjecture and the Magic of Kikuchi Graphs

A question that I am very interested in is whether it is possible to study hypergraphs with techniques that are in the spirit of spectral graph theory.

It is generally possible to “flatten” the adjacency tensor of a hypergraph into a matrix, especially if the hypergraph is ${k}$ -uniform with ${k}$ even, and spectral properties of this matrix give information about the hypergraph, but usually a large amount of information is lost in this process, and the approach can only be applied to rather dense hypergraphs.

If we have a 4-uniform hypergraph with ${n}$ vertices, for example, meaning a hypergraph in which each hyperedge is a set of four elements, its ${n \times n \times n \times n}$ adjacency tensor can be flattened to a ${n^2 \times n^2}$ matrix. Unless the hypergraph has a number of hyperedges that is at least quadratic in ${n}$ , however, such a matrix is too sparse to provide any useful information via basic spectral techniques.

Recently, a number of results of a “spectral hypergraph theory” flavor have appeared that, instead, apply spectral graph theory techniques to the Kikuchi graph associated to a hypergraph, leading to very impressive applications such as new lower bounds for locally correctable codes.

In this post I would like to show a simple but rather magical use of this approach, that gives a proof of Feige’s conjecture concerning a “Moore bound for hypergraphs”.

In an undirected graph, the girth is the length of the shortest simple cycle, and in the previous post we told the story of trade-offs between density of the graph and girth, such as the Moore bound.

In a hypergraph, an interesting analog to the notion of girth is the size of the smallest even cover, where an even cover is a set of hyperedges such that every vertex belongs to an even number of hyperedges in the set. The reader should spend a minute to verify that if the hypergraph is a graph, this definition is indeed equivalent to the girth of the graph.

To see why this is a useful property, the hyperedges of a ${k}$ -uniform hypergraph with vertex set V can be represented as vectors in ${{\mathbb F}_2^V}$ in a standard way: a vector ${x\in {\mathbb F}_2^V}$ represents the set ${\{ v : x_v \neq 0 \}}$ . Under this representation, an even cover is a collection of hyperedges whose corresponding vectors have a linear dependency, so a ${k}$ -uniform hypergraph with ${n}$ vertices, ${m}$ hyperedges and such that there is no even cover of size ${\leq L}$ corresponds to a construction of ${m}$ vectors in ${{\mathbb F}_2^n}$ , each of Hamming weight ${k}$ , such that any ${L}$ of them are linearly independent. Having large collections of sparse vectors that don’t have small linear dependencies is useful in several applications.

It is easy to study the size of even covers in random hypergraphs, and a number of results about CSP refutations and SoS lower bounds rely on such calculations. Feige made the following worst-case conjecture:

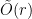
Conjecture 1 (Moore Bound for Hypergraphs) If a ${k}$ -uniform hypergraph has ${n}$ vertices and ${n\left( \frac{n}{r} \right) ^{\frac k2 -1}}$ hyperedges, then there must exist an even cover of size ${\tilde O( r )}$

Where the “tilde” hides a polylogn multiplicative factor. For ${k=3}$ , for example, the conjecture asserts that a hypergraph with ${n}$ vertices and ${m}$ hyperedges must contain an even cover of size ${\tilde O(n^3/m^2)}$ . For ${k=4}$ , the bound is ${\tilde O(n^2/m)}$ .

The Feige conjecture was recently proved by Guruswami, Kothari and Manohar using Kikuchi graphs and their associated matrices. In this post, we will see a simplified proof by Hsieh, Kothari and Mohanty (we will only see the even ${k}$ case, which is much easier to analyze, and we will not prove the case of odd ${k}$ , which is considerably more difficult).

1. A spectral proof of the Moore bound in graphs

We will first provide a spectral proof of the Moore bound for graphs, and then we will use Kikuchi graphs/matrices to lift the argument to hypergraphs.

To see how to use spectral arguments to reason about girth, let us start from the simple case of ${d}$ -regular graphs. We want to reason about cycles in a graph, and a spectral concept immediately comes to mind: if ${A}$ is the adjacency matrix of the graph, then ${{\rm tr}(A^L)}$ is the number of closed walks of length ${L}$ in the graph. If the girth of ${A}$ is more than ${L}$ , then none of those closed walks can be, or contain, a cycle, and this restricts how many such walks can exist. All such walks happen within the local tree that surrounds the start node, and the walk can just traverse part of this local tree. Combining these observations suffices to obtain a non-trivial bound.

First of all, if a graph is ${d}$ -regular, we have ${||A||=d}$ and so

$\displaystyle {\rm tr}(A^L) \geq ||A^L|| \geq d^L$

and we claim that if the girth is more than ${L}$ we also have

$\displaystyle {\rm tr} (A^L) \leq n\cdot 2^L \cdot (d-1)^{L/2}$

This is because a closed walk of even length ${L}$ , provided that ${L}$ is less than the girth, can be specified by indicating the starting node, of which there are ${n}$ , then for every step of the walk whether we are moving one step closer or one step further from the starting node in the local tree around the node, for which we have ${2^L}$ choices to enumerate, and, finally, for the ${L/2}$ steps in which we move one step further, which edge we follow, for which we have ${d-1}$ choices. When we move closer to the start node, only one edge can be followed and there are no choices to enumerate.

Combining the bounds and taking ${L}$ -th roots, we have ${2n^{1/L} \geq \sqrt {d}}$ , which gives the weak but respectable Moore-like bound

$\displaystyle L\leq 2\log_{d/4} n$

The next step is to make such an argument work for irregular graphs. We would again like to reason in terms of the trace of the power of a matrix, to relate it to counting closed walks, and to show that the count is small if the girth is large. We will need, however, to find the proper normalization, because we cannot use just the adjacency matrix any more.

If ${A}$ is the adjacency matrix of an irregular graph ${G}$ of average degree ${\bar d}$ and ${D}$ is the diagonal matrix of degrees of ${G}$ , so that ${D_{v,v} = d_v}$ is the degree of vertex ${v}$ , a common normalization is to look at the matrix ${D^{-1}A}$ , or to the symmetric matrix ${D^{-1/2} A D^{-1/2}}$ , which has the same trace and eigenvalues. This is also the transition matrix of the random walk in ${G}$ , so that when we study the trace of powers of this matrix we end up considering the probability that a random walk of a certain length returns to the start vertex. We also know that

$\displaystyle || D^{-1/2} A D^{-1/2} || = 1$

so that for every ${L}$

$\displaystyle {\rm tr}( (D^{-1/2} A D^{-1/2})^L) \geq ||( D^{-1/2} A D^{-1/2}) ^L|| \geq 1$

If we try to analyze the trace of powers of this matrix, however, we run into some technical difficulties, that are greatly simplified by a neat trick which is not totally natural and that I will try to justify.

Let us think about the regular case as analyzed above, except that we work with ${A/d}$ for consistency. The division by ${d}$ contributes a ${1/d^L}$ term to the trace of the ${L}$ -th power, so we “gain” a factor of ${1/d}$ in each step. We lose it almost entirely when we do a step away from the start node, because we have to account for ${d-1}$ choices, but we gain it entirely when we take a step closer to the start node, because that is a forced move for which we do not need to enumerate choices. We end up gaining a factor of ${1/d}$ for each backward step, of which there are ${L/2}$ , and so we can cleanly say that the trace goes down by a factor of ${d^{-L/2}}$ . We pay ${n}$ for the choice of the start vertex and ${2^L}$ for the choice of when to go forward and when to backward, and the overall bound is ${n 2^L d^{-L/2}}$ which becomes ${2 n^{1/L} / \sqrt d}$ when we take the ${L}$ -th root.

The difficulty in replicating this argument with the same cleanliness in the irregular case is that, when we are enumerating what can happen when the closed walk passes through a vertex ${v}$ , the gain from a backward step from ${v}$ is ${1/d_v}$ , which could be much larger than ${1/{\bar d}}$ , and it is not straightforward how to “average” things, because we are multiplying terms that are not independent.

It would certainly be very convenient if the normalization in a step from vertex ${v}$ was such that we always gain a factor that is both smaller than ${1/{\bar d}}$ , to have a proper account of the backward steps, and smaller than ${1/d_v}$ to account for the possible forward steps.

The trick is simply to enforce that with a different normalization: instead of working with ${D^{-1} A}$ or ${D^{-1/2} A D^{-1/2}}$ , we define ${\Gamma := \bar d \cdot I + D}$ and work with ${\Gamma ^{-1 }A}$ and ${\Gamma^{-1/2} A \Gamma^{-1/2}}$ . With this normalization, a step backward from ${v}$ contributes ${1/({\bar d} + d_v)}$ which is certainly less than ${1/{\bar d}}$ while the enumeration of steps forward can still not exceed a contribution of 1.

The only concern about this new normalization is that we divide ${A}$ by a larger matrix and this could cause its norm to drop too much, but fortunately the norm is essentially preserved, as we can see by using the test vector ${\Gamma ^{1/2} {\bf 1}}$ .

We have that the quadratic form is

$\displaystyle {\bf 1}^T \Gamma^{1/2} \Gamma ^{-1/2} A \Gamma^{-1/2} \Gamma ^{1/2} {\bf 1} = {\bf 1} ^TA {\bf 1} = {\bar d} n$

while the norm squared of the test vector is

$\displaystyle {\bf 1}^T \Gamma^{1/2} \Gamma^{1/2} {\bf 1} = {\bf 1}^T ( \bar d \cdot I + D) {\bf 1} = 2 {\bar d } n$

so that we have a good lower bound on the norm

$\displaystyle || \Gamma^{-1/2} A \Gamma^{-1/2} || \geq \frac 12$

To bound the trace of our normalized matrix, we perform a similar enumeration as the one we did in the regular case. We have to enumerate all closed walks ${v_0,v_1,\ldots,, v_{L-1},v_L}$ where ${v_0 = v_L}$ and the edge ${(v_i,v_{i+1}) }$ exists for ${i=0,\ldots,L-1}$ . We have ${n}$ choices for the start vertex ${v_0}$ and then ${2^L}$ choices for whether, at each step, we move one step closer to the start vertex in the local tree, in a unique way, or one step forward, in one of ${d_{v_i}-1}$ possible ways. We will denote by ${N_0(v_i)}$ the set containing the unique neighbor of ${v_i}$ that is one step closer to the start vertex in the local tree of the start vertex, and by ${N_1(v_i)}$ the set containing the ${d_v-1}$ neighbors of ${v_1}$ that are one step further. If ${b_v \in \{0,1\}}$ represents the binary choice of whether to move further or closer to the start vertex in the walk from node ${v}$ , then ${N_{b_v} (v)}$ is the set of choices that we have to enumerate.

With this notation we can write the trace as

$\displaystyle \begin{array}{rcl} & & {\rm tr}( (\Gamma^{-1} A)^L) \\ & = & \sum_{b \in \{ 0,1\}^L} \sum_{v_0 \in [n]} \sum_{v_1 \in N_{b_0}(v_0)}\Gamma^{-1}_{v_0,v_0} \ldots \\ & & \hspace{20pt} \sum_{v_{L-1} \in N_{b_{L-2}} (v_{L-2}) }\Gamma^{-1} _ { v_{L-2} ,v_{L-2} } \cdot {\bf 1}(v_0 \in N_{b_{L-1}} (v_{L-1})) \cdot \Gamma_{v_{L-1},v_{L-1}} \end{array}$

In order to bound the above expression, we see that we have ${2^L}$ choices for ${b}$ , then ${n}$ choices for ${v_0}$ , and for each of the ${L/2}$ steps from a vertex ${v_i}$ in which we go backward we have a term ${\Gamma^{-1} _{v_i,v_i}}$ which is ${1/(d_{v_i} + \bar d)< 1/\bar d}$ ; for each of the ${L/2}$ steps from a vertex ${v_i}$ in which we go forward we have ${d_{v_i}-1}$ branches, but each multiplied by ${1/(d_{v_i} + \bar d)< 1/d_{v_i}}$ so that the total contribution is less than 1.

Overall we can say

$\displaystyle \frac 1{2^L} < {\rm tr}( (\Gamma^{-1} A)^L) \leq n \cdot 2^L \cdot \bar d^{-L/2}$

so that rearranging and taking ${L}$ -th roots we have

$\displaystyle 4n^{1/L} > \sqrt {\bar d}$

that is also equivalent to

$\displaystyle L < 2\log_{\bar d/16} n$

which is again a respectable Moore-like bound for irregular graphs.

A final note about this spectral argument is that ${\Gamma^{-1} A}$ can still be seen as the transition matrix of a sort of random walk, that is, one that from ${v}$ has a probability ${\frac {\bar d}{\bar d + d_v}}$ of stopping, and probability ${\frac 1{\bar d + d_v}}$ of proceeding through each neighbor of ${v}$ . The trace of the ${L}$ -th power of ${\Gamma^{-1}A}$ computes, up to a factor of ${n}$ , the collision probability of the distribution of the ${(L/2)}$ -th step of this walk starting from a random vertex, and the negative logarithm of this probability is called the Renyi entropy of the distribution. This is all to say that this spectral argument is not totally unrelated to the argument in the previous post, in which we computed the entropy of a non-backtracking random walk started at a random vertex.

2. Kikuchi matrices and hypergraphs

We now come to the magic of this post, where we define Kikuchi graphs and associated matrices, and we see how to transfer spectral graph theory techniques to hypergraphs.

If ${H= ([n],F)}$ is a ${k}$ -uniform hypergraph with ${n}$ vertices, ${k}$ even, and if we select an integer parameter ${r \geq k/2}$ , the Kikuchi graph associated to ${H}$ and ${r}$ is a graph ${G= (V,E)}$ with ${|V| = {n \choose r}}$ vertices defined as follows. We think of each vertex of ${G}$ as a set ${S}$ of ${r}$ vertices of ${H}$ ; if ${e\in F}$ is a hyperedge of ${H}$ , then for every set ${S}$ of ${r}$ vertices we have the edge ${(S, S \oplus e)}$ in ${G}$ , where we use ${\oplus}$ to denote symmetric difference between sets. In other words, the edges of ${G}$ are the pairs of sets of ${r}$ vertices of ${H}$ whose symmetric difference is a hyperedge of ${H}$ .

This feels a lot like a Cayley graph, and in fact it can be seen as a vertex-induced subgraph of a Cayley graph, but this would not give a very enlightening perspective on the content of this post, so we will not pursue this concept furhter.

Necessarily, in an edge ${(S,T)}$ of the Kikuchi graph corresponding to an hyperedge ${e}$ , the sets ${S}$ and ${T}$ must each contain ${k/2}$ vertices of ${e}$ each, and so the construction as described only works for hypergraphs where the hyperedge cardinality is even. We already mentioned that everything becomes considerably more complex in the odd case, which we will not deal with.

For each hyperedge ${e}$ of ${H}$ , there are ${{k \choose k/2} \cdot {n-k \choose r-k/2}}$ choices of a set ${S}$ containing ${r}$ vertices of ${H}$ of which ${k/2}$ are from ${e}$ . Overall, if ${H}$ has ${m}$ hyperedges, ${G}$ is going to have

$\displaystyle \frac m2 \cdot {k \choose k/2} \cdot {n-k \choose r-k/2}$

undirected edges (the factor of 2 comes from the fact that without it we would count ${(S, S\oplus e)}$ and ${(S\oplus e, S)}$ as two different edges while it is the same undirected edge).

If ${r=k/2}$ , then the Kikuchi graph construction is analogous to the standard “flattening” of a tensor to a matrix or of a hypergraph to a graph, and it is not immediately clear from the definitions what is gained by choosing a larger ${r}$ and obtaining a larger graph that only seems more redundant and more complex to analyze.

An important gain is that for larger ${r}$ the resulting graph is denser. Indeed the average degree of the Kikuchi graph is

$\displaystyle \bar d = \frac m2 \cdot {k \choose k/2} \cdot {n-k \choose r-k/2} \cdot {n \choose r } ^{-1}$

and one can see that for ${ r > k}$ and ${r\leq n/8}$ the bound

$\displaystyle \bar d \geq \frac m2 \left ( \frac r n \right)^{k/2}$

holds, showing how larger choices of ${r}$ yield denser graphs.

What about even covers and Feige’s conjecture? Suppose ${H}$ does not have even covers of size ${\leq L}$ , and let us look at a length- ${L}$ closed walk ${S_0,S_1,\ldots S_L}$ in ${G}$ , where ${S_0 = S_L}$ and the edges ${(S_i,S_{i+1})}$ exist in ${G}$ for each step ${i=0,\ldots,L-1}$ of the walk. Let us call ${e_i}$ the hyperedge of ${H}$ corresponding to the edge ${(S_i,S_{i+1})}$ , so that we have ${S_i = S_{i+1} \oplus e_i}$ . The key observation is that, iterating the definitions of the edges we have

$\displaystyle S_L = S_0 \oplus e_0 \oplus e_1 \ldots \oplus e_{L-1}$

but we also have ${S_L=S_0}$ and so

$\displaystyle e_0 \oplus e_1 \ldots \oplus e_{L-1} = \emptyset$

From the multiset of hyperedges ${(e_0,\ldots e_{L-1} )}$ let us repeatedly remove pairs of identical hyperedges: this process will terminate either with a set of hyperedges occurring each once, or with an empty collection of hyperedges. The former case cannot happen, however, because this set of hyperedges would be a double cover of cadinality less than ${L}$ , so the process must terminate with an empty set, meaning that the multiset ${( e_0,\ldots e_{L-1} )}$ is such that every hyperedge occurs an even number of times.

Maybe it is not clear where we are going with this, but we have made all the key observations to be ready to prove the Feige conjecture, because we have related lack of even covers in the hypergraph with restricted properties of closed walks in the associated Kikuchi graph, and we already have spectral techniques that can be applied when we understand restrictions on closed walks in a graph.

3. Proof of the Feige Conjecture

The Feige conjecture will follow from the bounds formalized below:

Lemma 1 (Main) Let ${H}$ be an order ${k}$ , ${k}$ even, hypergraph with ${n}$ vertices and ${m}$ edges. Suppose that there is no even cover of size ${\leq L}$ in ${H}$ . Construct the Kikuchi graph ${G}$ of ${H}$ with parameter ${r}$ , where ${k < r < n/8}$ . Let ${A}$ be the adjacency matrix of ${G}$ , let ${D}$ be its diagonal matrix of degrees, let ${\bar d}$ be the average degree of ${G}$ , define ${\Gamma := \bar d \cdot I + D}$ . Then

$\displaystyle \frac 1 {2^L} \leq || ( \Gamma^{-1/2} A \Gamma^{-1/2} )^L || \leq {\rm tr}( ( \Gamma^{-1} A)^L) \leq n^r \cdot 2^L \cdot \left( \frac L {\bar d } \right) ^{L/2}$

We already proved the first two inequalities. To deal with the last one we will enumerate the closed walks of length ${L}$ in ${G}$ .

To enumerate all length- ${L}$ closed walks ${S_0,\ldots,S_{L-1}, S_L}$ with ${S_L=S_0}$ , we call ${e_i}$ the hyperedge associated to the edge ${(S_i,S_{i+1})}$ , and we again associate a vector ${b\in \{0,1\}^L}$ to each walk, but this time ${b_i=0}$ when the hyperedge ${e_i}$ is old, meaning it has already appeared in the sequence ${e_0,\ldots,e_{L-1}}$ as some ${e_j}$ with ${j<1}$ . We let ${b_i=1}$ if the hyperedge ${e_i}$ is new, meaning that it appears for the first time in the sequence ${e_0,\ldots,e_{L-1}}$ .

Note that now the Kikuchi graph does not necessarily have large girth: for example it is easy to see that it has a lot of length-4 cycles. From the discussion in the previous section, however, we know that the sequence ${e_0,\ldots,e_{L-1}}$ is such that every hyperedge that appears in the sequence appears an even number of times and, in particular, the sequence involves at most ${L/2}$ distinct hyperedges. This will be enough to obtain the claimed upper bound on the trace.

Analogously with the notation used in the previous section, We let ${N_{0} (S_i) }$ be the set of neighbors of ${S_i}$ that are possible as a next step of the closed walk assuming that the step ${(S_i,S_{i+1})}$ corresponds to an old hyperedge and ${N_{1} (S_i) }$ the set of neighbors of ${S_i}$ that are possible as a next step of the closed walk assuming that the step ${(S_i,S_{i+1})}$ corresponds to a new hyperedge.

With this notation, we can write the trace as

$\displaystyle \begin{array}{rcl} & & {\rm tr}( (\Gamma^{-1} A)^L) \\ & = & \sum_{b \in \{ 0,1\}^L} \sum_{S_0 \in {[n] \choose r}} \sum_{S_1 \in N_{b_0} (S_0)} \Gamma^{-1} _{S_0,S_0} \ldots \\ & & \hspace{15pt} \sum_{S_{L-1} \in N_{b_{L-2}} (S_{L-2}) }\Gamma^{-1} _{S_{L-2}, S_{L-2} } \cdot {\bf 1}( S_0 \in N_{b_{L-1}} (S_{L-1}) ) \cdot \Gamma^{-1} _{S_{L-1}, S_{L-1} } \end{array}$

We have ${2^L}$ choices for ${b}$ and ${{n \choose r} \leq n^r}$ choices for ${S_0}$ . For each step ${i}$ of the walk, if ${b_i = 0}$ and the step uses an old hyperedge, then ${N_0(S_i)}$ has at most ${i-1 \leq L}$ possibilities, corresponding to hyperedges that have been seen so far in the walk and that can be repeated. Each choice contributes a value of ${\Gamma^{-1}_{S_i,S_i} = \frac 1{d_{S_i} + \bar d} < \frac 1 {\bar d}}$ , for a total contribution that is at most ${\frac L{\bar d}}$ . Because all hyperedges that are used in the walk are used an even number of times, there have to be at least ${L/2}$ steps in which we have an old hyperedge. When ${b_i=1}$ and we have a new hyperedge at step ${i}$ , then ${N_1(S_i)}$ can be at most the set of all ${d_{S_i}}$ neighbors of ${S_i}$ , and each contributes a value of ${\Gamma^{-1}_{S_i,S_i} = \frac 1 {d_{S_i} + \bar d} < \frac 1 {d_{S_i}}}$ so that the total contribution is less than one. This proves the claimed upper bound

$\displaystyle 2^L n^r \left( \frac L {\bar d} \right)^{L/2}$

and establishes the Main Lemma.

After taking ${L}$ -th roots, the Main Lemma says that

$\displaystyle n^{r/L} \geq \frac 14 \sqrt{ \frac {\bar d}{L}}$

We instantiate the construction to

$\displaystyle r:= \frac L{\log_2 n}$

which makes ${n^{r/L} = 2}$ , so that the Main Lemma implies ${\bar d \leq 64 L}$ . Recall that we also proved

$\displaystyle \bar d \geq \frac m2 \left ( \frac r n \right)^{k/2}$

which combines to

$\displaystyle r\log_2 n = L \geq \frac {\bar d}{64} \geq \frac m{128} \left ( \frac r n \right)^{k/2}$

or, equivalently, we have proved the upper bound

$\displaystyle m \leq 128 n \log n \left( \frac nr \right)^{k/2 - 1}$

provided that there is no even cover of size ${\leq L = r \log_2 n}$ , which is precisely the Feige conjecture.

Without all the commentary that we added, the even case of the Feige conjecture, already a significant problem that had been open and challenging for a while, is solved in half a page of simple calculations. The magic of the Kikuchi graph comes in the very simple way that even covers in the hypergraph translate to restrictions to what closed walks can look like in the associated graph, and these are restrictions that are usefully exploitable in trace arguments.

As we remarked, something else that is also very useful in the connection is that the size of the sets corresponding to vertices in the Kikuchi graph is a parameter that we can control, and it “densifies” the graph the more it is turned up.

The odd ${k}$ case is considerably more involved, and it is where all the major work is done, though the even case already gives a glimpse of the power of these techniques.

I would like to remark that several technical steps above are taken verbatim from the paper of Hsieh, Kothari and Mohanty, as they are already as simplified and clear as they can be. I want to thank Lucas Pesenti for having explained this proof to me.

2 thoughts on “Feige’s Conjecture and the Magic of Kikuchi Graphs”

Simon Apers on April 28, 2024 at 8:34 pm said:

Thanks for another interesting post 🙂 It might be nice to provide links to some of the referenced papers.
luca on April 29, 2024 at 6:22 am said:

Thanks for the suggestion, I added some links

in theory

"Marge, I agree with you – in theory. In theory, communism works. In theory." — Homer Simpson

Feige’s Conjecture and the Magic of Kikuchi Graphs

2 thoughts on “Feige’s Conjecture and the Magic of Kikuchi Graphs”

Leave a comment

Share this:

Related

2 thoughts on “Feige’s Conjecture and the Magic of Kikuchi Graphs”

Leave a comment