A question that I am very interested in is whether it is possible to study hypergraphs with techniques that are in the spirit of spectral graph theory.
It is generally possible to “flatten” the adjacency tensor of a hypergraph into a matrix, especially if the hypergraph is  -uniform with
-uniform with  even, and spectral properties of this matrix give information about the hypergraph, but usually a large amount of information is lost in this process, and the approach can only be applied to rather dense hypergraphs.
even, and spectral properties of this matrix give information about the hypergraph, but usually a large amount of information is lost in this process, and the approach can only be applied to rather dense hypergraphs.
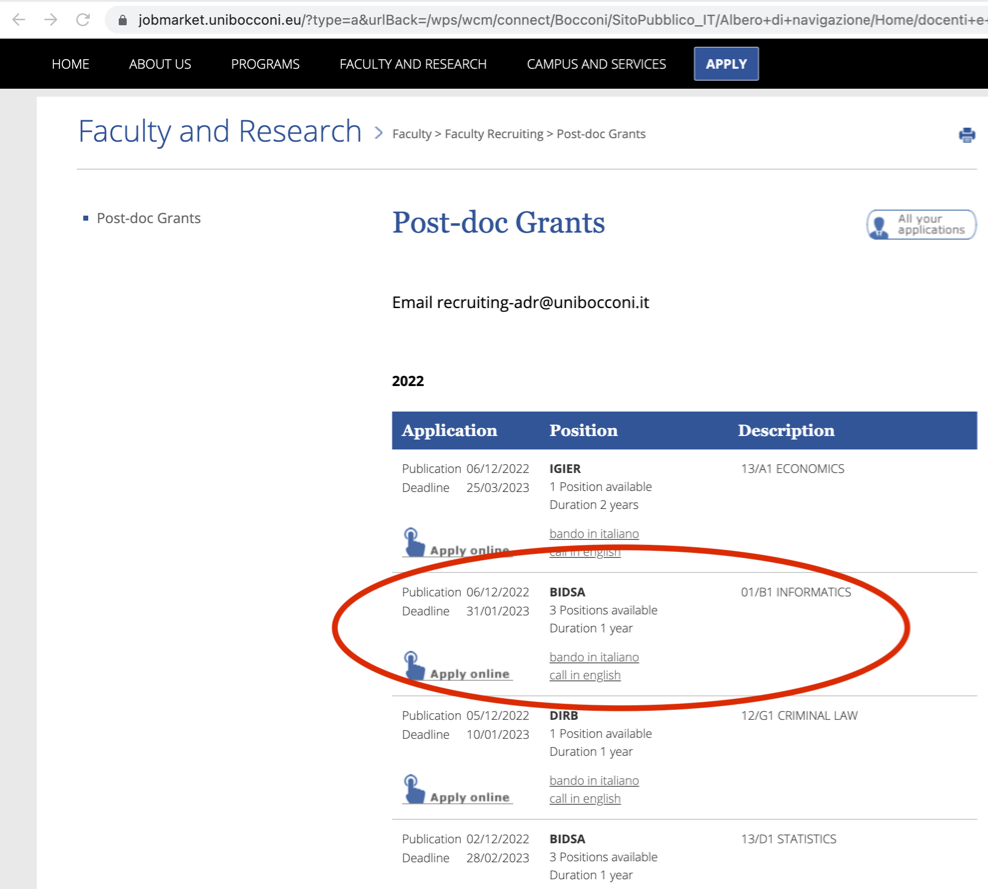
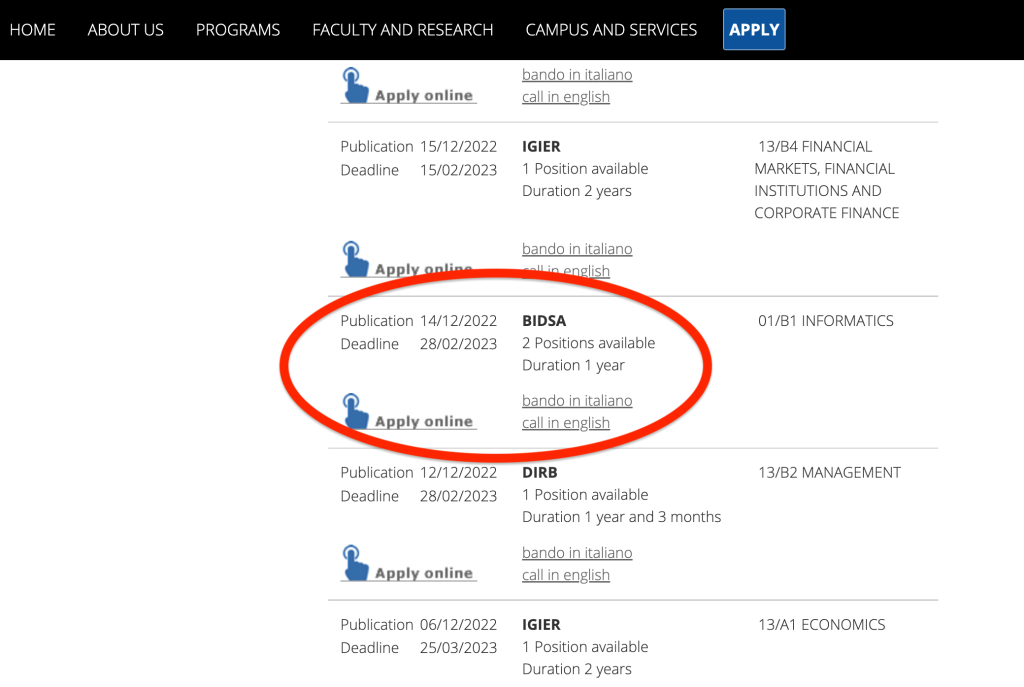
If we have a 4-uniform hypergraph with  vertices, for example, meaning a hypergraph in which each hyperedge is a set of four elements, its
vertices, for example, meaning a hypergraph in which each hyperedge is a set of four elements, its 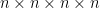 adjacency tensor can be flattened to a
adjacency tensor can be flattened to a 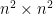 matrix. Unless the hypergraph has a number of hyperedges that is at least quadratic in
matrix. Unless the hypergraph has a number of hyperedges that is at least quadratic in  , however, such a matrix is too sparse to provide any useful information via basic spectral techniques.
, however, such a matrix is too sparse to provide any useful information via basic spectral techniques.
Recently, a number of results of a “spectral hypergraph theory” flavor have appeared that, instead, apply spectral graph theory techniques to the Kikuchi graph associated to a hypergraph, leading to very impressive applications such as new lower bounds for locally correctable codes.
In this post I would like to show a simple but rather magical use of this approach, that gives a proof of Feige’s conjecture concerning a “Moore bound for hypergraphs”.
In an undirected graph, the girth is the length of the shortest simple cycle, and in the previous post we told the story of trade-offs between density of the graph and girth, such as the Moore bound.
In a hypergraph, an interesting analog to the notion of girth is the size of the smallest even cover, where an even cover is a set of hyperedges such that every vertex belongs to an even number of hyperedges in the set. The reader should spend a minute to verify that if the hypergraph is a graph, this definition is indeed equivalent to the girth of the graph.
To see why this is a useful property, the hyperedges of a  -uniform hypergraph with vertex set V can be represented as vectors in
-uniform hypergraph with vertex set V can be represented as vectors in  in a standard way: a vector
in a standard way: a vector  represents the set
represents the set  . Under this representation, an even cover is a collection of hyperedges whose corresponding vectors have a linear dependency, so a
. Under this representation, an even cover is a collection of hyperedges whose corresponding vectors have a linear dependency, so a  -uniform hypergraph with
-uniform hypergraph with  vertices,
vertices, 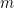 hyperedges and such that there is no even cover of size
hyperedges and such that there is no even cover of size  corresponds to a construction of
corresponds to a construction of 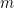 vectors in
vectors in 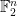 , each of Hamming weight
, each of Hamming weight  , such that any
, such that any 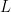 of them are linearly independent. Having large collections of sparse vectors that don’t have small linear dependencies is useful in several applications.
of them are linearly independent. Having large collections of sparse vectors that don’t have small linear dependencies is useful in several applications.
It is easy to study the size of even covers in random hypergraphs, and a number of results about CSP refutations and SoS lower bounds rely on such calculations. Feige made the following worst-case conjecture:
Conjecture 1 (Moore Bound for Hypergraphs) If a  -uniform hypergraph has
-uniform hypergraph has  vertices and
vertices and  hyperedges, then there must exist an even cover of size
hyperedges, then there must exist an even cover of size 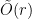
Where the “tilde” hides a polylogn multiplicative factor. For 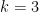 , for example, the conjecture asserts that a hypergraph with
, for example, the conjecture asserts that a hypergraph with  vertices and
vertices and 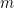 hyperedges must contain an even cover of size
hyperedges must contain an even cover of size  . For
. For  , the bound is
, the bound is  .
.
The Feige conjecture was recently proved by Guruswami, Kothari and Manohar using Kikuchi graphs and their associated matrices. In this post, we will see a simplified proof by Hsieh, Kothari and Mohanty (we will only see the even  case, which is much easier to analyze, and we will not prove the case of odd
case, which is much easier to analyze, and we will not prove the case of odd  , which is considerably more difficult).
, which is considerably more difficult).
Continue reading →