Today the Italian academic community, along with lots of other people, was delighted to hear that Giorgio Parisi is one of the three recipients of the 2021 Nobel Prize for Physics.
Parisi has been a giant in the area of understanding “complex” and “disordered” systems. Perhaps, his most influential contribution has been his “replica method” for the analysis of the Sherrington-Kirkpatrick model. His ideas have led to several breakthroughs in statistical physics by Parisi and his collaborators, and they have also found applications in computer science: to tight analyses on a number of questions about combinatorial optimization on random graphs, to results on random constraint satisfaction problems (including the famous connection with random k-SAT analyzed by Mezard, Parisi and Zecchina) and random error correcting codes, and to understanding the solution landscape in optimization problems arising from machine learning. Furthermore these ideas have also led to the development and analysis of algorithms.
The news was particularly well received at Bocconi, where most of the faculty of the future CS department has done work that involved the replica method. (Not to be left out, even I have recently used replica methods.)
Mezard and Montanari have written a book-length treatment on the interplay between ideas from statistical physics, algorithms, optimization, information theory and coding theory that arise from this tradition. Readers of in theory looking for a shorter exposition aimed at theoretical computer scientists will enjoy these notes posted by Boaz Barak, or this even shorter post by Boaz.
In this post, I will try to give a sense to the reader of what the replica method for the Sherrington-Kirkpatrick model looks like when applied to the average-case analysis of optimization problems, stripped of all the physics. Of course, without the physics, nothing makes any sense, and the interested reader should look at Boaz’s posts (and to references that he provides) for an introduction to the context. I did not have time to check too carefully what I wrote, so be aware that several details could be wrong.
What is the typical value of the max cut in a 
random graph with 
vertices?
Working out an upper bound using union bounds and Chernoff bound, and a lower bound by thinking about a greedy algorithm, we can quickly convince ourselves that the answer is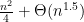 
. Great, but what is the constant in front of the 
? This question is answered by the Parisi formula, though this fact was not rigorously established by Parisi. (Guerra proved that the formula gives an upper bound, Talagrand proved that it gives a tight bound.)
Some manipulations can reduce the question above to the following question: suppose that I pick a random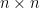 
symmetric matrix 
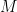, say with zero diagonal, and such that (up to the symmetry requirement) the entries are mutually independent and each entry is equally likely to be 
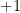or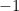 
, or perhaps each entry is distributed according to a standard normal distribution (the two versions can be proved to be equivalent), what is the typical value of
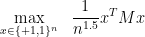
up to 
additive terms,?
As a first step, we could replace the maximum with a “soft-max,” and note that, for every choice of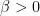 
, we have
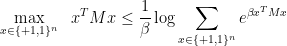
The above upper bound gets tighter and tighter for larger 
, so if we were able to estimate
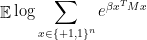
for every (where the expectation is over the randomness of 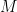) then we would be in good shape.
We could definitely use convexity and write
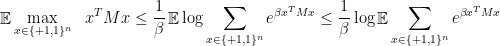
and then use linearity of expectation and independence of the entries of 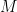to get to
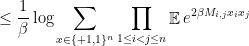
Now things simplify quite a bit, because for all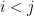 
the expression 
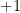, in the Rademacher setting, is equally likely to be or 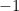, so that, for 
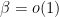, we have
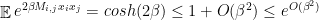
and
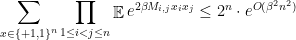
so that
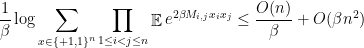
which, choosing 
, gives an 
upper bound which is in the right ballpark. Note that this is exactly the same calculations coming out of a Chernoff bound and union bound. If we optimize the choice of we unfortunately do not get the right constant in front of .
So, if we call
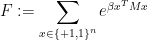
we see that we lose too much if we do the step
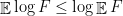
But what else can we do to get rid of the logarithm and to reduce to an expression in which we take expectations of products of independent quantities (if we are not able to exploit the assumption that 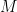has mutually independent entries, we will not be able to make progress)?
The idea is that if 
is a small enough quantity (something much smaller than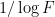 
), then 
is close to 1 and we have the approximation
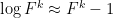
and we obviously have
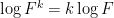
so we can use the approximation
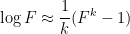
and
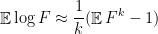
Let’s forget for a moment that we want 
to be a very small parameter. If was an integer, we would have
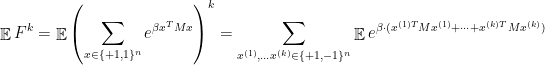
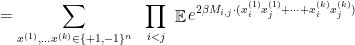
Note that the above expression involves choices of -tuples of feasible solutions of our maximization problem. These are the “replicas” in “replica method.”
The above expression does not look too bad, and note how we were fully able to use the independence assumption and “simplify” the expression. Unfortunately, it is actually still very bad. In this case it is preferable to assume the 
to be Gaussian, write the expectation as an integral, do a change of variable and some tricks so that we reduce to computing the maximum of a certain function, let’s call it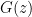 
, where the input 
is a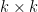 
matrix, and then we have to guess what is an input of maximum value for this function. If we are lucky, the maximum is equivalent by a in which all entries are identical, the replica symmetric solution. In the Sherrington-Kirkpatrick model we don’t have such luck, and the next guess is that the optimal is a block-diagonal matrix, or a replica symmetry-breaking solution. For large , and large number of blocks, we can approximate the choice of such matrices by writing down a system of differential equations, the Parisi equations, and we are going to assume that such equations do indeed describe an optimal and so a solution to the integral, and so they give as a computation of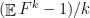 
.
After all this, we get an expression for 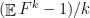for every sufficiently large integer , as a function of up to lower order errors. What next? Remember how we wanted to be a tiny real number and not a sufficiently large integer? Well, we take the expression, we forget about the error terms, and we set 
in theory 