Tag Archives: semidefinite programming

Beyond Worst Case Analysis: Lecture 4

Posted on by
1

Scribed by Rachel Lawrence

In which we introduce semidefinite programming and apply it to Max Cut.

1. Overview

We begin with an introduction to Semidefinite Programming (SDP). We will then see that, using SDP, we can find a cut with the same kind of near-optimal performance for Max Cut in random graphs as we got from the greedy algorithm — that is,

\displaystyle cut > \frac{|E|}{2} + \Omega(n\cdot\sqrt[]{d})

in random graphs {G_n, \frac{d}{n}}. More generally, we will prove that you can always find a cut at least this large in the case that G is triangle-free and with maximum vertex degree {\geq d}, which will imply the bound in random graphs. We will also see how to use SDP to certify an upper bound:

\displaystyle max\ cut < \frac{|E|}{2} + O(n\cdot \sqrt[]{d})

with high probability in {G_{n, \frac{d}{n}}}

Methods using SDP will become particularly helpful in future lectures when we consider planted-solution models instead of fully random graphs: greedy algorithms will fail on some analogous problems where methods using SDP can succeed.

2. Semidefinite Programming

Semidefinite Programming (SDP) is a form of convex optimization, similar to linear programming but with the addition of a constraint stating that, if the variables in the linear program are considered as entries in a matrix, that matrix is positive semidefinite. To formalize this, we begin by recalling some basic facts from linear algebra.

2.1. Linear algebra review

Definition 1 (Positive Semidefinite) A matrix {M\in {\mathbb R}^{n \times n}} is positive semidefinite (abbreviated PSD and written {M \succeq {\bf 0}}) if it is symmetric and all its eigenvalues are non-negative.

We will also make use of the following facts from linear algebra:

  1. If {M \in {\mathbb R}^{n \times n}} is a symmetric matrix, then all the eigenvalues of {M} are real, and, if we call {\lambda_1 \leq \lambda_2 \leq \cdots \leq \lambda_n} the eigenvalues of {M} with repetition, we have

    \displaystyle M = \sum_i \lambda_i {\bf v}^{(i)} ({\bf v}^{(i)})^T

    where the {{\bf v}^{(i)}} are orthonormal eigenvectors of the {\lambda_i}.

  2. The smallest eigenvalue of {M} has the characterization

    \displaystyle \lambda_1 = \min_{{\bf y} \neq {\bf 0}} \frac{{\bf y}^T M {\bf y}}{||{\bf y}||^2}

    and the optimization problem in the right-hand side is solvable up to arbitrarily good accuracy

This gives us the following lemmas:

Lemma 2 {M \succeq {\bf 0}} if and only if for every vector {{\bf y}} we have {{\bf y}^T M {\bf y} \geq 0}.

Proof: From part (2) above, the smallest eigenvalue of M is given by

\displaystyle \lambda_1 = \min_{{\bf y} \neq {\bf 0}} \frac{{\bf y}^T M {\bf y}}{||{\bf y}||^2}

Noting that we always have {||{\bf y}||^2 \geq 0}, then {\lambda_1 \geq 0} if and only if the numerator {{\bf y}^T M {\bf y}} on the right is always non-negative. \Box

Lemma 3 If {A, B \succeq {\bf 0}}, then {A + B \succeq {\bf 0}}

Proof: {\forall {\bf y}}, {{\bf y}^T (A+B) {\bf y} = {\bf y}^T A {\bf y} + {\bf y}^T B {\bf y} \geq 0}. By Lemma 2, this implies {A+B \succeq 0}. \Box

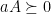
Lemma 4 If {A \succeq 0} and {a \geq 0}, then {aA \succeq 0}

Proof: {\forall y}, {{\bf y}^T a A {\bf y} = a({\bf y}^T A {\bf y}) \geq 0}. By Lemma 2, this implies {aA \succeq 0}. \Box

2.2. Formulation of SDP

With these characterizations in mind, we define a semidefinite program as an optimization program in which we have {n^2} real variables {X_{i,j}}, with {1 \leq i,j \leq n}, and we want to maximize, or minimize, a linear function of the variables such that linear constraints over the variables are satisfied (so far this is the same as a linear program) and subject to the additional constraint that the matrix {X} is PSD. Thus, a typical semidefinite program (SDP) looks like

\displaystyle \begin{array}{rcl} \max && \sum_{i,j} C_{i,j} X_{i,j} \\ s.t.\\ && \sum_{i,j} A^{(1)}_{i,j} X_{i,j} \leq b_1\\ && \vdots\\ && \sum_{i,j} A^{(m)}_{i,j} X_{i,j} \leq b_m\\ && X \succeq {\bf 0} \end{array}

where the matrices {C,A^{(1)},\ldots, A^{(m)}} and the scalars {b_1,\ldots,b_m} are given, and the entries of {X} are the variables over which we are optimizing.

We will also use the following alternative characterization of PSD matrices

Lemma 5 A matrix {M\in {\mathbb R}^{n \times n}} is PSD if and only if there is a collection of vectors {{\bf x}^{(1)},\ldots, {\bf x}^{(n)}} such that, for every {i,j}, we have {M_{i,j} = \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle }.

Proof: Suppose that {M} and {{\bf x}^{(1)},\ldots, {\bf x}^{(n)}} are such that {M_{i,j} = \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle } for all {i} and {j}. Then {M} is PSD because for every vector {{\bf y}} we have

\displaystyle {\bf y}^T M {\bf y} = \sum_{i,j} y_i y_j M_{i,j} = \sum_{i,j} y_iy_j \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle = \left\|\sum_i y_i {\bf x}^{(i)} \right\|^2 \geq 0

Conversely, if {M} is PSD and we write it as

\displaystyle M = \sum_k \lambda_k {\bf v}^{(k)} ({\bf v}^{(k)})^T

we have

\displaystyle M_{i,j} = \sum_k \lambda_k v^{(k)}_i v_j^{(k)}

and we see that we can define {n} vectors {{\bf x}^{(1)},\cdots,{\bf x}^{(n)}} by setting

\displaystyle x^{(i)}_k := \sqrt {\lambda_k} \cdot v^{(k)}_i

and we do have the property that

\displaystyle M_{i,j} = \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle

\Box

This leads to the following equivalent formulation of the SDP optimization problem:

\displaystyle \begin{array}{rcl} \max && \sum_{i,j} C_{i,j}\langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle \\ s.t.\\ && \sum_{i,j} A^{(1)}_{i,j} \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle \leq b_1\\ && \vdots\\ && \sum_{i,j} A^{(m)}_{i,j} \langle {\bf x}^{(i)}, {\bf x}^{(j)}\rangle \leq b_m\\ \end{array}

where our variables are vectors {{\bf x}^{(1)},\cdots,{\bf x}^{(n)}}. This is the statement of the optimization problem that we will most commonly use.

2.3. Polynomial time solvability

From lemmas 3 and 4, we recall that if {A} and {B} are two matrices such that {A\succeq {\bf 0}} and {B \succeq {\bf 0}}, and if {a\geq 0} is a scalar, then {a \cdot A \succeq {\bf 0}} and {A+B \succeq 0}. This means that the set of PSD matrices is a convex subset of {{\mathbb R}^{n \times n}}, and that the above optimization problem is a convex problem.

Using the ellipsoid algorithm, one can solve in polynomial time (up to arbitrarily good accuracy) any optimization problem in which one wants to optimize a linear function over a convex feasible region, provided that one has a separation oracle for the feasible region: that is, an algorithm that, given a point,

  1. Checks whether it is feasible and, if not,
  2. Constructs an inequality that is satisfied by all feasible point but not satisfied by the given point.

In order to construct a separation oracle for a SDP, it is enough to solve the following problem: given a matrix {M}, decide if it is PSD or not and, if not, construct an inequality {\sum_{ij}a_{ij}x_{ij} \geq 0} that is satisfied by the entries of all PSD matrices but that is not satisfied by {M}. In order to do so, recall that the smallest eigenvalue of {M} is

\displaystyle \min_{{\bf y}} \frac {{\bf y}^T M {\bf y} }{|| {\bf y}||^2 }

and that the above minimization problem is solvable in polynomial time (up to arbitrarily good accuracy). If the above optimization problem has a non-negative optimum, then {M} is PSD. If it is a negative optimum {{\bf y}^*}, then the matrix is not PSD, and the inequality

\displaystyle \sum_{i,j} X_{i,j} y^*_i y^*_j \geq 0

is satisfied for all PSD matrices {X} but fails for {X:= M}. Thus we have a separation oracle and we can solve SDPs in polynomial time up to arbitrarily good accuracy.

3. SDP Relaxation of Max Cut and Random Hyperplane Rounding

The Max Cut problem in a given graph {G=(V,E)} has the following equivalent characterization, as a quadratic optimization problem over real variables {x_1,\ldots,x_n}, where {V = \{ 1,\ldots,n\}}:

\displaystyle \begin{array}{rcl} {\rm MaxCut} (G) =& \max & \sum_{(i,j) \in E} \frac 14 (x_i - x_j)^2 \\ & s.t.\\ && x_i^2 = 1 \ \ \ \ \ \forall i \in V \end{array}

We can interpret this as associating every vertex {v} with a value {x_v = \pm 1}, so that the cut edges are those with one vertex of value {+1} and one of value {-1}.

While quadratic optimization is NP-hard, we can instead use a relaxation to a polynomial-time solvable problem. We note that any quadratic optimization problem has a natural relaxation to an SDP, in which we relax real variables to take vector values and we change multiplication to inner product:

\displaystyle \begin{array}{rcl} {\rm MaxCut} (G) \leq & \max & \sum_{(i,j) \in E} \frac 14 || {\bf x}_i - {\bf x}_j ||^2 \\ & s.t.\\ && || {\bf x}_i|| ^2 = 1 \ \ \ \ \ \forall i \in V \end{array}

Figure 1: The hyperplane through the origin defines a cut partitioning the vertices into sets {\{x_1, x_2\}} and {\{x_3, x_4\}}.

Solving the above SDP, which is doable in polynomial time up to arbitrarily good accuracy, gives us a unit vector {{\bf x}_i} for each vertex {i}. A simple way to convert this collection to a cut {(S,V-S)} is to take a random hyperplane through the origin, and then define {S} to be the set of vertices {i} such that {{\bf x}_i} is above the hyperplane. Equivalently, we pick a random vector {{\bf g}} according to a rotation-invariant distribution, for example a Gaussian distribution, and let {S} be the set of vertices {i} such that {\langle {\bf g}, {\bf x}_i \rangle \geq 0}.

Let {(i,j)} be an edge: One sees that if {\theta} is the angle between {{\bf x}_i} and {{\bf x}_j}, then the probability {(i,j)} is cut is proportional to {\theta}:

\displaystyle \mathop{\mathbb P} [ (i,j) \mbox{ is cut } ] = \frac {\theta}{\pi}

and the contribution of {(i,j)} to the cost function is

\displaystyle \frac 14 || {\bf x}_i - {\bf x}_j ||^2 = \frac 12 - \frac 12 \langle {\bf x}_i , {\bf x}_j \rangle = \frac 12 - \frac 12 \cos \theta

Some calculus shows that for every {0 \leq \theta \leq \pi} we have

\displaystyle \frac {\theta}{\pi} > .878 \cdot \left( \frac 12 - \frac 12 \cos \theta \right)

and so

\displaystyle \mathop{\mathbb E} [ \mbox{ number of edges cut by } (S,V-S) ] \geq .878 \cdot \sum_{(i,j) \in E} \frac 14 || {\bf x}_i - {\bf x}_j ||^2

\displaystyle = .878 \cdot {\rm SDPMaxCut}(G) \geq .878 \cdot {\rm MaxCut} (G)

so we have a polynomial time approximation algorithm with worst-case approximation guarantee {.878}.

Next time, we will see how the SDP relaxation behaves on random graphs, but first let us how it behaves on a large class of graphs.

4. Max Cut in Bounded-Degree Triangle-Free Graphs

Theorem 6 If {G= (V,E)} is a triangle-free graph in which every vertex has degree at most {d}, then

\displaystyle MaxCut(G) \geq \left( \frac 12 +\Omega \left( \frac 1 {\sqrt d} \right) \right) \cdot |E|

Proof: Consider the following feasible solution for the SDP: we associate to each node {i} an {n}-dimensional vector {{\bf x}^{(i)}} such that {x^{(i)}_i = \frac 1{\sqrt 2}}, {x^{(i)}_j = -1/\sqrt{2deg(i)}} if {(i,j) \in E}, and {x^{(i)}_j = 0} otherwise. We immediately see that {||{\bf x}^{(i)} ||^2 = 1} for every {i} and so the solution is feasible.

For example, if we have a graph such that vertex 1 is adjacent to vertices 3 and 5:

{1} 2 3 4 5 {\cdots}
{x^{(1)}: } {\frac 1{\sqrt 2}} 0 {-\frac{1}{\sqrt[]{2deg(1)}}} 0 {-\frac{1}{\sqrt[]{2deg(1)}}}
{x^{(2)}: } 0 {\frac 1{\sqrt 2}} 0 0 0
{x^{(3)}: } {-\frac{1}{\sqrt[]{2deg(3)}}} 0 {\frac 1{\sqrt 2}} 0 0
{\vdots} {\vdots}
{x^{(n)}: } 0 0 0 0 0 {\cdots}

Let us transform this SDP solution into a cut {(S,V-S)} using a random hyperplane.

We see that, for every edge {(i,j)} we have

\displaystyle \langle {\bf x}^{(i)}, {\bf x}^{(j)} \rangle = - \frac 1 {\sqrt{2d(i)}} - \frac 1 {\sqrt{2d(j)}} \leq - \frac 1 {\sqrt d}

The probability that {(i,j)} is cut by {(S,V-S)} is

\displaystyle \frac { \arccos \left( \frac 12 - \frac 1 {2 \sqrt d} \right ) }{\pi}

and

\displaystyle \frac { \arccos \left( \frac 12 - \frac 1 {2 \sqrt d} \right )}{\pi } = \frac 12 + \frac {\arcsin \left( \frac 1 {2 \sqrt d} \right) }{\pi} \geq \frac 12 + \Omega \left( \frac 1 {\sqrt d} \right)

so that the expected number of cut edges is at least {\left( \frac 12 + \Omega \left( \frac 1 {\sqrt d} \right) \right) \cdot |E|}. \Box

Two recent papers by Cui Peng

Posted on by
8

Cui Peng of Renmin University in Beijing has recently released two preprints, one claiming a proof of P=NP and one claiming a refutation of the Unique Games Conjecture; I will call them the “NP paper” and the “UG paper,” respectively.

Of all the papers I have seen claiming a resolution of the P versus NP problem, and, believe me, I have seen a lot of them, these are by far the most legit. On Scott Aronson’s checklist of signs that a claimed mathematical breakthrough is wrong, they score only two.

Unfortunately, both papers violate known impossibility results.

The two papers follow a similar approach: a certain constraint satisfaction problem is proved to be approximation resistant (under the assumption that P{\neq}NP, or under the UGC, depending on the paper) and then a Semidefinite Programming approximation algorithm is developed that breaks approximation resistance. (Recall that a constraint satisfaction problem is approximation resistant if there is no polynomial time algorithm that has a worst-case approximation ratio better than the algorithm that picks a random assignment.)

In both papers, the approximation algorithm is by Hast, and it is based on a semidefinite programming relaxation studied by Charikar and Wirth.

The reason why the results cannot be correct is that, in both cases, if the hardness result is correct, then it implies an integrality gap for the Charikar-Wirth relaxation, which makes it unsuitable to break the approximation resistance as claimed.

Suppose that we have a constraint satisfaction problem in which every constraint is satisfied by a {p} fraction of assignment. Then for such a problem to not be approximation resistant, we have to devise an algorithm that, for some fixed positive {\delta>0}, returns a solution whose cost (the number of constraints that it satisfies) is at least {p+\delta} times the optimum. The analysis of such an algorithm needs to include some technique to prove upper bounds for the true optimum; this is because if you are given an instance in which the optimum satisfies at most a {p+o(1)} fraction of constraints, as is the case for a random instance, then the algorithm will satisfy at most a {p+o(1)} fraction of constraints, but then the execution of the algorithm and the proof of correctness will give a (polynomial-time computable and polynomial-time checkable) certificate that the optimum satisfies at most a {(p+o(1))/(p+\delta) < 1 - \delta + o(1)} fraction of constraints.

For algorithms that are based on relaxations, such certificates came from the relaxation itself: one shows that the algorithm satisfies a number of constraints that is at least {p+\delta} times the optimum of the relaxation, and the optimum of the relaxation is at least the optimum of the constraint satisfaction problem. But if there are instances for which the optimum is {p+o(1)} and the optimum of the relaxation is {1-o(1)}, then one cannot use such a relaxation to design an algorithm that breaks approximation-resistance. (Because on, such instances, the algorithm will not be able to satisfy a number of constraint equal to {p+\delta} times the optimum of the relaxation.)

In the UG paper, the approximation resistance relies on a result of Austrin and Håstad. Like all UGC-based inapproximability results that I am aware of, the hardness results of Austrin and Håstad are based on a long code test. A major result of Raghavendra is that for every constraint satisfaction problem one can write a certain SDP relaxation such that the integrality gap of the relaxation is equal to the ratio between soundness and completeness in the best possible long code test that uses predicates from the constraint satisfaction problem. In particular, in Section 7.7 of his thesis, Prasad shows that if you have a long code test with soundness {c} and completeness {s} for a constraint satisfaction problem, then for every {\epsilon > 0} there is an instance of the problem in which no solution satisfies more than {s+\epsilon} fraction of constraints, but there is a feasible SDP solution whose cost is at least a {c-\epsilon} fraction of the number of constraints. The SDP relaxation of Charikar and Wirth is the same as the one studied by Prasad. This means that if you prove, via a long code test, that a certain problem is approximation resistant, then you also show that the SDP relaxation of Charikar and Wirth cannot be used to break approximation resistance.

The NP paper adopts a technique introduced by Siu On Chan to prove inapproximability results by starting from a version of the PCP theorem and then applying a “hardness amplification” reduction. Tulsiani proves that if one proves a hardness-of-approximation result via a “local” approximation-reduction from Max 3LIN, then the hardness-of-approximation result is matched by an integrality gap for Lasserre SDP relaxations up to a super-constant number of rounds. The technical sense in which the reduction has to be “local” is as follows. A reduction from Max 3LIN (the same holds for other problems, but we focus on starting from Max 3LIN for concreteness) to another constraint satisfaction problems has two parameters: a “completeness” parameter {c} and a “soundness” parameter {s}, and its properties are that:

  • (Completeness Condition) the reduction maps instances of 3LIN in which the optimum is {1-o(1)} to instances of the target problem in which the optimum is at least {c-o(1)};
  • (Soundness Condition) the reduction maps instances of 3LIN in which the optimum is {1/2 +o(1)} to instances of the target problem in which the optimum is at most {s+o(1)}.

Since we know that it’s NP-hard to distinguish Max 3LIN instances in which the optimum is {1-o(1)} from instances in which the optimum is {1/2 +o(1)}, such a reduction shows that, in the target problem, it is NP-hard to distinguish instances in which the optimum is {c-o(1)} from instances in which the optimum is {s+o(1)}. The locality condition studied by Tulsiani is that the Completeness Condition is established by describing a mapping from solutions satisfying a {1-o(1)} fractions of the Max 3LIN constraints to solutions satisfying a {c-o(1)} fraction of the target problem constraints, and the assignment to each variable of the target problem can be computed by looking at a sublinear (in the size of the Max 3LIN instance) number of Max 3LIN variables. Reductions that follows the Chan methodology are local in the above sense. This means that if one proves that a problem is approximation-resistant using the Chan methodology starting from the PCP theorem, then one has a local reduction from Max 3LIN to the problem with completeness {1-o(1)} and soundness {p+o(1)}, where, as before, {p} is the fraction of constraints of the target problem satisfied by a random assignment. In turn, this implies that not just the Charikar-Wirth relaxation, but that, for all relaxations obtained in a constant number of rounds of Lasserre relaxations, there are instances of the target problem that have optimum {p+o(1)} and SDP optimum {1-o(1)}, so that the approximation resistance cannot be broken using such SDP relaxations.