Bounded Independence, AC0, and Random 3SAT

Posted on January 23, 2009 by luca

As reported here, here and here, Mark Braverman has just announced a proof of a 1990 conjecture by Linial and Nisan.

Mark proves that if ${C}$ is an AC0 boolean circuit (with NOT gates and with AND gates and OR gates of unbounded fan-in) of depth ${d}$ and size ${S}$ , and if ${X}$ is any ${k}$ -wise independent distribution with ${k = (\log S)^{O(d^2)}}$ , then

$\displaystyle {\mathbb E} C(U_n) \approx {\mathbb E} C(X)$

that is, ${X}$ “fools” the circuit ${C}$ into thinking that ${X}$ is the uniform distribution ${U_n}$ over ${\{0,1\}^n}$ . Plausibly, this might be true even for ${k = O((\log S)^{d-1})}$ .

Nothing was known for depth 3 or more, and the depth-2 case was settled only recently by Bazzi, with a proof that, as you may remember, has been significantly simplified by Razborov about six months ago.

Mark’s proof relies on approximating ${C}$ via low-degree polynomials. The point is that if ${p}$ is an ${n}$ -variate (real valued) polynomial of degree ${\leq k}$ , and ${X}$ is a ${k}$ -wise independent distribution ranging over ${\{0,1\}^n}$ , then

$\displaystyle {\mathbb E} p(X) = {\mathbb E} p(U_n)$

Now if we could show that ${p}$ approximates ${C}$ both under ${X}$ and under ${U_n}$ , in the sense that ${{\mathbb E} p(X) \approx {\mathbb E} C(X)}$ , and also ${{\mathbb E} p(U_n) \approx {\mathbb E} C(U_n)}$ , then we would be done.

The Razborov-Smolenski lower bound technique gives a probabilistic construction of a polynomial ${p}$ such that for every input ${x}$ one has a high probability that ${p(x) = C(x)}$ . In particular, one get one polynomial ${p}$ such that both

$\displaystyle {\mathbb P}_{x\sim X} [p(x) = C(x) ] = 1-o(1) \ \ \ \ \ (1)$

and

$\displaystyle {\mathbb P}_{x\sim U_n} [p(x) = C(x) ] = 1-o(1) \ \ \ \ \ (2)$

Unfortunately this is not sufficient, because the polynomial ${p}$ might be very large at a few points, and so even if ${p}$ agrees with ${C}$ with high probability there is no guarantee that the average of ${p}$ is close to the average of ${C}$ .

Using a result of Linial, Mansour and Nisan (developed in the context of learning theory), one can construct a different kind of low-degree approximating polynomial ${p}$ , which is such that

$\displaystyle {\mathbb E}_{x\sim U_n} | C(x) - p(x)|^2 = o(1) \ \ \ \ \ (3)$

The Linial-Mansour-Nisan approximation, however, says nothing about the relation between ${p}$ and ${C}$ under the distribution ${X}$ .

Using ideas of Bazzi’s, however, if we had a single polynomial ${p}$ such that properties (1), (2) and (3) are satisfied simultaneously, then we could construct another low-degree polynomial ${p'}$ such that ${{\mathbb E} p'(X) \approx {\mathbb E} C(X)}$ , and also ${{\mathbb E} p'(U_n) \approx {\mathbb E} C(U_n)}$ , giving us that ${C}$ is fooled by ${X}$ .

As far as I understand, Mark constructs a polynomial satisfying properties (1), (2) and (3) by starting from the Razborov-Smolenski polynomial ${p}$ , and then observing that the indicator function ${E}$ of the points on which ${p \neq C}$ is itself a boolean function admitting a Linial-Mansour-Nisan approximation ${e}$ . Defining ${p' := p\cdot (1-e)}$ , we have that ${p'}$ has all the required properties, because multiplying by ${1-e}$ “zeroes out” the points on which ${p}$ is excessively large.

I have been interested in this problem for some time because of a connection with the complexity of 3SAT on random instances.

As I have discussed in the past, if we take a random instance of 3SAT constructed by randomly picking, say, 10n clauses over n variables, then there is an extremely high probability that the formula is unsatisfiable. Certifying that such formulas are unsatisfiable, however, appears to be hard.

Here what we want is a certification algorithm ${A}$ that, on input a boolean formula ${\phi}$ , outputs either unsatisfiable or don’t know; if the algorithm outputs unsatisfiable then the formula is definitely guaranteed to be unsatisfiable; and the algorithm outputs unsatisfiable on at least, say, a ~~inverse polynomial~~ constant fraction of inputs. (Thanks for Albert Atserias for pointing out that the problem is trivial if one requires only inverse polynomial refutation probability.)

The existence of such an algorithm for random 3SAT with ${n}$ variables and ${10n}$ clauses has been ruled out in a variety of bounded models of computation. (And of course the lower bounds extend to higher number of clauses than ${10n}$ .) For example, we know that, except with very small probability, no sub-exponential size “tree-like resolution” proof of unsatisfiability can exist for formulas from this distribution, and we know that when a back-tracking based algorithm finishes without having found a satisfying assignment, its computation defines a tree-like resolution proof. Hence no back-tracking based algorithm can run in sub-exponential time. We also know lower bounds for algorithms based on convex relaxations of Max 3SAT, including algorithms based on Lasserre semidefinite programming relaxations, which are about the most powerful convex programming relaxations that we know how to construct.

Notably, I don’t know of a lower bound showing that no such refutation algorithm can be designed in AC0, even though AC0 is a class for which we are usually able to prove lower bounds. (As far as I know, the question remains open.)

All the above lower bounds, by the way, apply also to random instances of the 3XOR problem with, say, n variables and 10n equations. (3XOR is like 3SAT but every “clause” is a linear equation mod 2 involving three variables.) 3XOR is of course solvable in polynomial time via Gaussian elimination, but in many simplified models of computation it seems to capture the hardness of 3SAT.

So what about refuting random 3XOR in AC0? Consider the following two distributions of instances:

Distribution ${A}$ contains random instances with ${n}$ variables, ${10n}$ clauses, and uniformly chosen right-hand-side
Distribution ${B}$ contains instances with a random left-hand side involving ${n}$ variables and ${10n}$ clauses, and a right-hand side chosen to be consistent with a random assignment.

Now the left-hand side has the same distribution in ${A}$ and ${B}$ , and for, most left-hand-sides, the distribution of the right-hand side in ${B}$ in ${\Omega(n)}$ -wise independent, while the right-hand side in ${A}$ is always uniform.

From Mark’s result it follows that ${A}$ and ${B}$ are indistinguishable by AC0 circuits, and so no AC0 circuit can refute random instances from distribution ${B}$ . (Otherwise it would incorrectly output unsatisfiable with positive probability given samples from ${B}$ , while all samples from ${B}$ are satisfiable.)

18 thoughts on “Bounded Independence, AC0, and Random 3SAT”

x on January 23, 2009 at 1:53 pm said:

Should k in the third line be (log S)^O(d^2)?
luca on January 23, 2009 at 2:46 pm said:

thanks
Pingback: News « Combinatorics and more
Abhishek Bhowmick on January 24, 2009 at 10:01 pm said:

Referring to the 7^{th} line, wasn’t the possibility of k=(log S)^{d-1} ruled out by Luby and Velickovic in 1996?
Gil Kalai on January 24, 2009 at 10:24 pm said:

Here is a problem (perhaps silly) that comes to mind: Is the conclusion of the Linial-Nisan conjecture (=Braverman’s result) holds for monotone $TC^0$ , namely for bounded depth circuits with (monotone) threshold gates?
luca on January 25, 2009 at 12:33 am said:

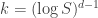There is a counterexample by Mansour (cited in the Luby-Velickovic paper), but it has to do with the relation between the “epsilon” in epsilon-pseudorandom and the “k” in k-wise independence. The example shows that, for depth 2, one needs at least $\log (1/\epsilon) * \log S$ – wise independence in order to fool depth-2. It remains possible than one can have constant epsilon with $k = (\log S)^{d-1}$ .

Gil, bounded independence does not seem to be the right notion to fool monotone $TC^0$ . Take the distribution over n-bit strings which is uniform over strings whose bits xor to 0. This is (n-1)-wise independent,
but it is concentrated on strings with an even number of zeroes. In particular,
the probability of, say, having more than n/2 +1 ones is going to be off by
$\Omega(1/\sqrt(n))$ . This means that (n-1)-wise independence is
not sufficient to fool *depth-1* monotone $TC^0$ .
elad on January 25, 2009 at 6:28 am said:

Luca and Gil: maybe a better notion is being epsilon-biased? Can a (1/poly)-biased generator fool monotone TC^0. (I don’t even remember whether it fools one threshold gate. I think it does for some range of epsilons, but not up to eps=1/poly. But I’m not sure).

Does any PRG that fools one threshold gate fool all TC0 circuits? Might be related to a recent result by Rabani and Shpilka:

Click to access RabaniShpilka08.pdf
Gil on January 25, 2009 at 6:36 am said:

Dear Luca. Thanks !
I suppose I can only mean “to fool” in the weak sense that the averages cannot be bounded away from each other as n tends to infinity. (But this may still be silly.) Is this false as well?

(maybe if you fool it by 1/sqrt n you can amplify it to a constant; but i dont see it off-hand)

The reason for it is this: a naive (incorrect) argument for Linial-Nisan is that since LMN’s theorem asserts that the Fourier coefficients of f in AC0 decay exponentially abovd (log size)^depth, it should be fooled by a distribution whose Fourier coefficients are supported only above
polylog (size).

For monotone TC0 circuits it is conjectured that the fourier coefficients decay above (log size)^poly(depth) (This looks very hard.) Here we cannot hope for exponential decay (false already for majority) but perhaps to a decay of the form n^-beta.
luca on January 25, 2009 at 11:09 am said:

Elad, epsilon-biased doesn’t work either: consider the uniform distribution over bits strings with a number of ones which is a multiple of 3. It is epsilon-biased with exponentially small epsilon, but, for small i, the probability of being larger than n/2 + i is wrong by an additive term $\approx 1/{\sqrt n}$
elad on January 26, 2009 at 2:55 pm said:

Ah, that’s a really simple example. Thanks!

After a bit more thinking, I have a very negative answer to myself (and a partial answer to Gil as well):

To myself: I was wondering whether TC0 can be fooled up to a constant by a 1/poly-biased generator. That’s false. The inner product function can be computed by TC0, and cannot be fooled by epsilon-biased generators, even up to constant error. (i.e. there is an eps-biased PRG that doesn’t fool it — the one which is uniform on the 1-set of the inner product function).

To Gil: This means that almost-k-wise independence doesn’t work for TC0, when the almost is very-very-almost, i.e. the generator I give above is inverse-exponentially close to being k-wise independent for any reasonable k. However, I don’t have a perfectly-k-wise independent distribution that fails to fool the inner product function even up to a constant, although I would suspect that one exists. (Maybe be making a small correction to the above distribution, potentially by working on a smaller set of variables and using the remaining ones to do the correction).

On the positive side: about monotone TC0: thresholds are known to be fooled to within any constant by O(1)-wise independence. (I think the right reference is “On k-wise independent events and percolation” by Benjamini, Gurevich and Peled, but I didn’t re-check right now, so don’t take my word for it). So, conceivably, it could be that O(polylog(n))-wise independence also fools monotone TC0 up to any constant (or slightly sub-constant) error. Somehow, this makes sense, but as Gil says, it looks hard to prove.
elad on January 26, 2009 at 3:11 pm said:

by the way, there’s a ton of other nice questions that one can ask now that Braverman’s Theorem is proved, all of which are probably hard. Here are a few:

1. Is it true that any function whose spectrum is concentrated on the first k levels and decays exponentially thereafter, is fooled by poly(k)-wise independence? That would mean that k-wise independence is a good analogue to the low-degree learner.

2. If #1 is true, maybe even the following is true: Can you prove that if 1-eps of the Fourier mass of f is found in a set of poly(n) coefficients, then any (eps/poly(n))-biased PRG fools f? When I say mass I mean in L_2 norm. Yes, I know that the common wisdom says that L_2 norm says nothing about PRGs, but somehow this seems plausible to me. This would mean that eps-biased generators are a good analogue to the sparse learner.

3. What about ACC0[2]? Now you have no LMN-type characterization, and Andrej also says that no hard function for ACC0[2] is known (Luca?). But I already said that these are hard.
a on January 27, 2009 at 9:23 am said:

well, since we’re somewhat on the topic, hopefully someone can clarify something that has bugged me for years: what is the “opposite direction” of Impagliazzo Wigderson? I’ve seen this referred to many times as “optimal conversion of hardness into randomness”.

First let us recall IW. I will try to be precise with the quantifiers:
Assumption: For some c, delta, there is a function uniformly computable in time $2^{c n}$ which is not computable by any circuit of size
$2^{\delta n}$.
Conclusion: Then for any t, there is a PRG computable in time
$n^{f(c, delta, t)}$ that fools all circuits of size $n^{t}$.

The reverse should be something like: show me a PRG with so and so parameters, and I will show you a function which is so and so hard.

and this optimal hardness should be enough to go back to IW and produce the same strength PRG again? Is that what they mean?
Then it should be a uniformly computable function in E hard for $2^{delta n}$ size circuits.

Probably you want to take a bit of the PRG and claim it is a hard function of the seed. But that isn’t so clear, as some of the bits may equal certain bits of the seed. Uniformly, how would you figure out which bit to take?
luca on January 27, 2009 at 6:56 pm said:

You look at the first seedlength+1 output bits of the generator, and you
check whether they are a possible output of the generator or not.

In more detail:

————–
Suppose you have a generator as in IW, mapping m bits into
2^{Omega(m)} bits, having 2^{\gamma m} security, and being
uniformly computable in time 2^{O(m)}.

(The parameter m here is (t/gamma)*log n, where t and n are as
in your statement of the conclusion of IW.)

Indeed, let us restrict ourselves to the first m+1 output bits
of the generator. This is a generator mapping m bits to m+1 bits
with the same pseudorandomness as before. Define the
boolean function F, that on input m+1 bits, decides whether they
are a possible output of the generator. This is uniformly computable
in time at most 2^m times the running time of the generator, so
it is uniformly computable in time 2^{O(m)} overall.

Any algorithm that computes F, however, is a distinguisher
for the truncated generator, and so F must have circuit complexity 2^{Omega(n)}.
luca on January 27, 2009 at 7:08 pm said:

Elad, it is known that computing majority and computing mod 3 are both
hard for ACC0[2].

For ACC0[p], p prime, it is known that mod q, where q is a different prime,
is hard.

The open problem is proving a lower bound for ACC0[m], m composite.
The first interesting case is ACC0[6], which, for all we know, could
contain all of NEXP.

Also, I don’t think your #2 can be true. Fix a very sparse epsilon/poly(n)
biased distribution, and let f be the constant 0 on the support of the
pseudorandom distribution and the constant 1 elsewhere.

Then all but an exponentially small fraction of the Fourier mass of f is
concentrated on the empty coefficient, because the function is exponentially
close to a constant in L2 norm, but it is definitely not fooled.
Pingback: …fool me ε times, shame on my constant-depth circuit | mathemagicio.us
elad on March 3, 2009 at 12:06 pm said:

Luca — thanks for the corrections! (better late than never…)
elad on March 6, 2009 at 10:10 am said:

“better late than never” refers to my reply, not to the correction.
Pingback: The attention economy for scientific work « Algorithmic Game Theory

in theory

"Marge, I agree with you – in theory. In theory, communism works. In theory." — Homer Simpson

Bounded Independence, AC0, and Random 3SAT

18 thoughts on “Bounded Independence, AC0, and Random 3SAT”

Leave a comment

Share this:

Related

18 thoughts on “Bounded Independence, AC0, and Random 3SAT”

Leave a comment