In which we analyze the zig-zag graph product.
In the previous lecture, we claimed it is possible to “combine” a -regular graph on
vertices and a
-regular graph on
vertices to obtain a
-regular graph on
vertices which is a good expander if the two starting graphs are. Let the two starting graphs be denoted by
and
respectively. Then, the resulting graph, called the zig-zag product of the two graphs is denoted by
.
We will use to denote the eigenvalue with the second-largest absolute value of the normalized adjacency matrix
of a
-regular graph
. If
are the eigenvalues of the normalized Laplacian of
, then
.
We claimed that if and
, then
. In this lecture we shall recall the construction for the zig-zag product and prove this claim.
1. Replacement Product and Zig-Zag Product
We first describe a simpler product for a “small” -regular graph on
vertices (denoted by
) and a “large”
-regular graph on
vertices (denoted by
). Assume that for each vertex of
, there is some ordering on its
neighbors. Then we construct the replacement product (see figure)
as follows:
- Replace each vertex of
with a copy of
(henceforth called a cloud). For
, let
denote the
vertex in the
cloud.
- Let
be such that
is the
-th neighbor of
and
is the
-th neighbor of
. Then
. Also, if
, then
.
Note that the replacement product constructed as above has vertices and is
-regular.

2. Zig-zag product of two graphs
Given two graphs and
as above, the zig-zag product
is constructed as follows (see figure):
- The vertex set
is the same as in the case of the replacement product.
-
if there exist
and
such that
,
and
are in
i.e.
can be reached from
by taking a step in the first cloud, then a step between the clouds and then a step in the second cloud (hence the name!).

It is easy to see that the zig-zag product is a -regular graph on
vertices.
Let be the normalized adjacency matrix of
. Using the fact that each edge in
is made up of three steps in
, we can write
as
, where
And if
is the
-th neighbor of
and
is the
-th neighbor of
, and
otherwise.
Note that is the adjacency matrix for a matching and is hence a permutation matrix.
3. A Technical Preliminary
We will use the following fact. Suppose that is the normalized adjacency matrix of a graph
. Thus the largest eigenvalue of
is 1, with eigenvector
; we have
which is a corollary of the following more general result. Recall that a vector space is an invariant subspace for a matrix
if
for every
.
Lemma 1 Let
be a symmetric matrix, and
be a
-dimensional invariant subspace for
. Thus, (from the proof of the spectral theorem) we have that
has an orthonormal basis of eigenvectors; let
be the corresponding eigenvalues with multiplicities; we have
Proof: If the largest eigenvalue in absolute value is , then
and if it is (because
is negative, and
)
From Cauchy-Schwarz, we have
Finally, if is the basis of orthonormal eigenvectors in
such that
, then, for every
, we can write
and
and the Lemma follows by combining (2), (3) and (4).
4. Analysis of the zig-zag Product
Theorem 2 Let
be a
-regular graph with
nodes,
be a
-regular graph with
nodes, and let
,
, and let the normalized adjacency matrix of
be
where
and
are as defined in Section 1.
Then
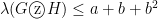
Proof: Let be such that
. We refer to a set of coordinates of
corresponding to a copy of
as a “block” of coordinate.
We write , where
is constant within each block, and
sums to zero within each block. Note both
and
are orthogonal to
, and that they are orthogonal to each other.
We want to prove
We have (using the fact that is symmetric)
And it remains to bound the three terms.
-
Because, after writing
, we see that
, because
is the same as
, the tensor product of the identity and of the normalized adjacency matrix of
. The normalized adjacency matrix of
leaves a vector parallel to all-ones unchanged, and so
leaves every vector that is constant in each block unchanged.
Thus
Let
be the vector such that
is equal to the value that
has in the block of
. Then
because
and
-
Because, from Cauchy-Schwarz and the fact that permutation matrices preserve length, we have
Now let us call
the restriction of
to coordinates of the form
for
. Then each
is orthogonal to the all-one vector and
, so
-
Because, from Cauchy-Schwarz, the fact that
and the fact that permutation matrices preserve length, we have
and we proved above that
so
