Scribed by Luowen Qian
In which we use spectral techniques to find certificates of unsatisfiability for random  -SAT formulas.
-SAT formulas.
1. Introduction
Given a random  -SAT formula with
-SAT formula with 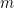 clauses and
clauses and  variables, we want to find a certificate of unsatisfiability of such formula within polynomial time. Here we consider
variables, we want to find a certificate of unsatisfiability of such formula within polynomial time. Here we consider  as fixed, usually equal to 3 or 4. For fixed
as fixed, usually equal to 3 or 4. For fixed  , the more clauses you have, the more constraints you have, so it becomes easier to show that these constraints are inconsistent. For example, for 3-SAT,
, the more clauses you have, the more constraints you have, so it becomes easier to show that these constraints are inconsistent. For example, for 3-SAT,
- In the previous lecture, we have shown that if
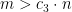 for some large constant
for some large constant  , almost surely the formula is not satisfiable. But it’s conjectured that there is no polynomial time, or even subexponential time algorithms that can find the certificate of unsatisfiability for
, almost surely the formula is not satisfiable. But it’s conjectured that there is no polynomial time, or even subexponential time algorithms that can find the certificate of unsatisfiability for 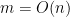 .
.
- If
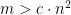 for some other constant
for some other constant  , we’ve shown in the last time that we can find a certificate within polynomial time with high probability that the formula is not satisfiable.
, we’ve shown in the last time that we can find a certificate within polynomial time with high probability that the formula is not satisfiable.
The algorithm for finding such certificate is shown below.
- Algorithm 3SAT-refute(
 )
)
- for

- if 2SAT-satisfiable(
 restricted to clauses that contains
restricted to clauses that contains  , with
, with  )
)
- return
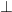
- return UNSATISFIABLE
We know that we can solve 2-SATs in linear time, and approximately

clauses contains 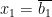 . Similarly when
. Similarly when  is sufficiently large, the 2-SATs will almost surely be unsatisfiable. When a subset of the clauses is not satisfiable, the whole 3-SAT formula is not satisfiable. Therefore we can certify unsatisfiability for 3-SATs with high probability.
is sufficiently large, the 2-SATs will almost surely be unsatisfiable. When a subset of the clauses is not satisfiable, the whole 3-SAT formula is not satisfiable. Therefore we can certify unsatisfiability for 3-SATs with high probability.
In general for  -SAT,
-SAT,
- If
 for some large constant
for some large constant 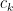 , almost surely the formula is not satisfiable.
, almost surely the formula is not satisfiable.
- If
 for some other constant
for some other constant  , we can construct a very similar algorithm, in which we check all assignments to the first
, we can construct a very similar algorithm, in which we check all assignments to the first 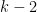 variables, and see if the 2SAT part of the restricted formula is unsatisfiable.
variables, and see if the 2SAT part of the restricted formula is unsatisfiable.
Since for every fixed assignments to the first 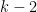 variables, approximately
variables, approximately

portion of the 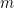 clauses remains, we expect the constant
clauses remains, we expect the constant 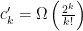 and the running time is
and the running time is  .
.
So what about 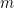 ‘s that are in between? It turns out that we can do better with spectral techniques. And the reason that spectral techniques work better is that unlike the previous method, it does not try all the possible assignments and fails to find a certificate of unsatisfiability.
‘s that are in between? It turns out that we can do better with spectral techniques. And the reason that spectral techniques work better is that unlike the previous method, it does not try all the possible assignments and fails to find a certificate of unsatisfiability.
2. Reduce certifying unsatisfiability for k-SAT to finding largest independent set
2.1. From 3-SAT instances to hypergraphs
Given a random 3-SAT formula  , which is an and of
, which is an and of 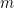 random 3-CNF-SAT clauses over
random 3-CNF-SAT clauses over  variables
variables  (abbreviated as vector
(abbreviated as vector  ), i.e.
), i.e.

where ![{\sigma_{i,j} \in [n], b_{i,j} \in \{0, 1\}}](https://s0.wp.com/latex.php?latex=%7B%5Csigma_%7Bi%2Cj%7D+%5Cin+%5Bn%5D%2C+b_%7Bi%2Cj%7D+%5Cin+%5C%7B0%2C+1%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) ,
, ![{\forall i \in [m], \sigma_{i,1} < \sigma_{i,2} < \sigma_{i,3}}](https://s0.wp.com/latex.php?latex=%7B%5Cforall+i+%5Cin+%5Bm%5D%2C+%5Csigma_%7Bi%2C1%7D+%3C+%5Csigma_%7Bi%2C2%7D+%3C+%5Csigma_%7Bi%2C3%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) and no two
and no two 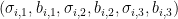 are exactly the same. Construct hypergraph
are exactly the same. Construct hypergraph 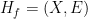 , where
, where
![\displaystyle X = \left\{(i, b) \middle| i \in [n], b \in \{0, 1\}\right\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+X+%3D+%5Cleft%5C%7B%28i%2C+b%29+%5Cmiddle%7C+i+%5Cin+%5Bn%5D%2C+b+%5Cin+%5C%7B0%2C+1%5C%7D%5Cright%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is a set of  vertices, where each vertex means an assignment to a variable, and
vertices, where each vertex means an assignment to a variable, and
![\displaystyle E = \left\{ e_j \middle| j \in [m] \right\}, e_j = \{(\sigma_{j,1}, \overline{b_{j,1}}), (\sigma_{j,2}, \overline{b_{j,2}}), (\sigma_{j,3}, \overline{b_{j,3}})\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+E+%3D+%5Cleft%5C%7B+e_j+%5Cmiddle%7C+j+%5Cin+%5Bm%5D+%5Cright%5C%7D%2C+e_j+%3D+%5C%7B%28%5Csigma_%7Bj%2C1%7D%2C+%5Coverline%7Bb_%7Bj%2C1%7D%7D%29%2C+%28%5Csigma_%7Bj%2C2%7D%2C+%5Coverline%7Bb_%7Bj%2C2%7D%7D%29%2C+%28%5Csigma_%7Bj%2C3%7D%2C+%5Coverline%7Bb_%7Bj%2C3%7D%7D%29%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is a set of 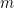 3-hyperedges. The reason we’re putting in the negation of
3-hyperedges. The reason we’re putting in the negation of  is that a 3-CNF clause evaluates to false if and only if all three subclauses evaluate to false. This will be useful shortly after.
is that a 3-CNF clause evaluates to false if and only if all three subclauses evaluate to false. This will be useful shortly after.
First let’s generalize the notion of independent set for hypergraphs.
An independent set for hypergraph  is a set
is a set  that satisfies
that satisfies  .
.
If  is satisfiable,
is satisfiable,  has an independent set of size at least
has an independent set of size at least  . Equivalently if the largest independent set of
. Equivalently if the largest independent set of  has size less than
has size less than  ,
,  is unsatisfiable. Proof: Assume
is unsatisfiable. Proof: Assume  is satisfiable, let
is satisfiable, let  be a satisfiable assignment, where
be a satisfiable assignment, where 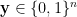 . Then
. Then ![{S = \{ (x_i, y_i) | i \in [n] \}}](https://s0.wp.com/latex.php?latex=%7BS+%3D+%5C%7B+%28x_i%2C+y_i%29+%7C+i+%5Cin+%5Bn%5D+%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is an independent set of size
is an independent set of size  . If not, it means some hyperedge
. If not, it means some hyperedge 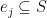 , so
, so  and the
and the  -th clause in
-th clause in  evaluates to false. Therefore
evaluates to false. Therefore  evaluates to false, which contradicts the fact that
evaluates to false, which contradicts the fact that 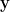 is a satisfiable assignment.
is a satisfiable assignment. 
We know that if we pick a random graph that’s sufficiently dense, i.e. the average degree  , by spectral techniques we will have a certifiable upper bound on the size of the largest independent set of
, by spectral techniques we will have a certifiable upper bound on the size of the largest independent set of  with high probability. So if a random graph has
with high probability. So if a random graph has 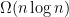 random edges, we can prove that there’s no large independent set with high probability.
random edges, we can prove that there’s no large independent set with high probability.
But if we have a random hypergraph with 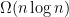 random hyperedges, we don’t have any analog of spectral theories for hypergraphs that allow us to do this kind of certification. And from the fact that the problem of certifying unsatisfiability of random formula of
random hyperedges, we don’t have any analog of spectral theories for hypergraphs that allow us to do this kind of certification. And from the fact that the problem of certifying unsatisfiability of random formula of 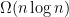 clauses is considered to be hard, we conjecture that there doesn’t exist a spectral theory for hypergraphs able to replicate some of the things we are able to do on graphs.
clauses is considered to be hard, we conjecture that there doesn’t exist a spectral theory for hypergraphs able to replicate some of the things we are able to do on graphs.
However, what we can do is possibly with some loss, to reduce the hypergraph to a graph, where we can apply spectral techniques.
2.2. From 4-SAT instances to graphs
Now let’s look at random 4-SATs. Similarly we will write a random 4-SAT formula  as:
as:

where ![{\sigma_{i,j} \in [n], b_{i,j} \in \{0, 1\}}](https://s0.wp.com/latex.php?latex=%7B%5Csigma_%7Bi%2Cj%7D+%5Cin+%5Bn%5D%2C+b_%7Bi%2Cj%7D+%5Cin+%5C%7B0%2C+1%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) ,
, ![{\forall i \in [m], \sigma_{i,1} < \sigma_{i,2} < \sigma_{i,3} < \sigma_{i,4}}](https://s0.wp.com/latex.php?latex=%7B%5Cforall+i+%5Cin+%5Bm%5D%2C+%5Csigma_%7Bi%2C1%7D+%3C+%5Csigma_%7Bi%2C2%7D+%3C+%5Csigma_%7Bi%2C3%7D+%3C+%5Csigma_%7Bi%2C4%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) and no two
and no two  are exactly the same. Similar to the previous construction, but instead of constructing another hypergraph, we will construct just a graph
are exactly the same. Similar to the previous construction, but instead of constructing another hypergraph, we will construct just a graph 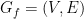 , where
, where
![\displaystyle V = \left\{(i_1, b_1, i_2, b_2) \middle| i_1, i_2 \in [n], b_1, b_2 \in \{0, 1\}\right\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+V+%3D+%5Cleft%5C%7B%28i_1%2C+b_1%2C+i_2%2C+b_2%29+%5Cmiddle%7C+i_1%2C+i_2+%5Cin+%5Bn%5D%2C+b_1%2C+b_2+%5Cin+%5C%7B0%2C+1%5C%7D%5Cright%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is a set of  vertices and
vertices and
![\displaystyle E = \left\{ e_j \middle| j \in [m] \right\}, e_j = \{(\sigma_{j,1}, \overline {b_{j,1}}, \sigma_{j,2}, \overline {b_{j,2}}), (\sigma_{j,3}, \overline {b_{j,3}}, \sigma_{j,4}, \overline {b_{j,4}})\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+E+%3D+%5Cleft%5C%7B+e_j+%5Cmiddle%7C+j+%5Cin+%5Bm%5D+%5Cright%5C%7D%2C+e_j+%3D+%5C%7B%28%5Csigma_%7Bj%2C1%7D%2C+%5Coverline+%7Bb_%7Bj%2C1%7D%7D%2C+%5Csigma_%7Bj%2C2%7D%2C+%5Coverline+%7Bb_%7Bj%2C2%7D%7D%29%2C+%28%5Csigma_%7Bj%2C3%7D%2C+%5Coverline+%7Bb_%7Bj%2C3%7D%7D%2C+%5Csigma_%7Bj%2C4%7D%2C+%5Coverline+%7Bb_%7Bj%2C4%7D%7D%29%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is a set of 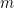 edges.
edges.
If  is satisfiable,
is satisfiable,  has an independent set of size at least
has an independent set of size at least 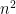 . Equivalently if the largest independent set of
. Equivalently if the largest independent set of  has size less than
has size less than 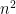 ,
,  is unsatisfiable. Proof: The proof is very similar to the previous one. Assume
is unsatisfiable. Proof: The proof is very similar to the previous one. Assume  is satisfiable, let
is satisfiable, let  be a satisfiable assignment, where
be a satisfiable assignment, where 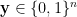 . Then
. Then ![{S = \{ (x_i, y_i, x_j, y_j) | i, j \in [n] \}}](https://s0.wp.com/latex.php?latex=%7BS+%3D+%5C%7B+%28x_i%2C+y_i%2C+x_j%2C+y_j%29+%7C+i%2C+j+%5Cin+%5Bn%5D+%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is an independent set of size
is an independent set of size 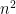 . If not, it means some edge
. If not, it means some edge 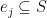 , so
, so 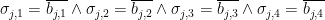 and the
and the  -th clause in
-th clause in  evaluates to false. Therefore
evaluates to false. Therefore  evaluates to false, which contradicts the fact that
evaluates to false, which contradicts the fact that 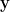 is a satisfiable assignment.
is a satisfiable assignment. 
From here, we can observe that  is not a random graph because some edges are forbidden, for example when the two vertices of the edge has some element in common. But it’s very close to a random graph. In fact, we can apply the same spectral techniques to get a certifiable upper bound on the size of the largest independent set if the average degree
is not a random graph because some edges are forbidden, for example when the two vertices of the edge has some element in common. But it’s very close to a random graph. In fact, we can apply the same spectral techniques to get a certifiable upper bound on the size of the largest independent set if the average degree  , i.e. if
, i.e. if  , we can certify unsatisfiability with high probability, by upper bounding the size of the largest independent set in the constructed graph.
, we can certify unsatisfiability with high probability, by upper bounding the size of the largest independent set in the constructed graph.
We can generalize this results for all even  ‘s. For random
‘s. For random  -SAT where
-SAT where  is even, if
is even, if 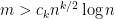 , we can certify unsatisfiability with high probability, which is better than the previous method which requires
, we can certify unsatisfiability with high probability, which is better than the previous method which requires  . The same
. The same  is achievable for odd
is achievable for odd  , but the argument is significantly more complicated.
, but the argument is significantly more complicated.
2.3. Certifiable upper bound for independent sets in modified random sparse graphs
Despite odd  ‘s, another question is that in this setup, can we do better and get rid of the
‘s, another question is that in this setup, can we do better and get rid of the 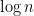 term? This term is coming from the fact that spectral norm break down when the average degree
term? This term is coming from the fact that spectral norm break down when the average degree 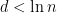 . However it’s still true that random graph doesn’t have any large independent sets even when the average degree
. However it’s still true that random graph doesn’t have any large independent sets even when the average degree  is constant. It’s just that the spectral norm isn’t giving us good bounds any more, since the spectral norm is at most
is constant. It’s just that the spectral norm isn’t giving us good bounds any more, since the spectral norm is at most  . So is there something tighter than spectral bounds that could help us get rid of the
. So is there something tighter than spectral bounds that could help us get rid of the 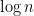 term? Could we fix this by removing all the high degree vertices in the random graph?
term? Could we fix this by removing all the high degree vertices in the random graph?
This construction is due to Feige-Ofek. Given random graph  , where the average degree
, where the average degree 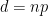 is some large constant. Construct
is some large constant. Construct 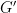 by taking
by taking  and removing all edges incident on nodes with degree higher than
and removing all edges incident on nodes with degree higher than  where
where  is the average degree of
is the average degree of  . We denote
. We denote  for the adjacency matrix of
for the adjacency matrix of  and
and  for that of
for that of 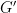 . And it turns out,
. And it turns out,
With high probability,  .
.
It turns out to be rather difficult to prove. Previously we saw spectral results on random graphs that uses matrix traces to bound the largest eigenvalue. In this case, it’s hard to do so because the contribution to the trace of a closed walk is complicated by the fact that edges have dependencies. The other approach is that given random matrix 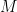 , we will try to upper bound
, we will try to upper bound  . A standard way for this is to that for every solution, count the instances of
. A standard way for this is to that for every solution, count the instances of 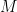 in which the fixed solution is good, and argue that the number of the fixed solutions is small, which tells us that there’s no good solution. The problem here is that the set of solutions is infinitely large. So Feige-Ofek discretize the set of vectors, and then reduce the bound on the quadratic form of a discretized vector to a sum of several terms, each of which has to be carefully bounded.
in which the fixed solution is good, and argue that the number of the fixed solutions is small, which tells us that there’s no good solution. The problem here is that the set of solutions is infinitely large. So Feige-Ofek discretize the set of vectors, and then reduce the bound on the quadratic form of a discretized vector to a sum of several terms, each of which has to be carefully bounded.
We always have

and so, with high probability, we get an 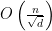 polynomial time upper bound certificate to the size of the independent set for a
polynomial time upper bound certificate to the size of the independent set for a  random graph. This removes the extra
random graph. This removes the extra 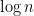 term from our analysis of certificates of unsatisfiability for random
term from our analysis of certificates of unsatisfiability for random  -SAT when
-SAT when  is even.
is even.
3. SDP relaxation of independent sets in random sparse graphs
In order to show a random graph has no large independent sets, a more principled way is to argue that there is some polynomial time solvable relaxation of the problem whose solution is an upper bound of the problem.
Let SDPIndSet be the optimum of the following semidefinite programming relaxation of the Independent Set problem, which is due to Lovász:
be the optimum of the following semidefinite programming relaxation of the Independent Set problem, which is due to Lovász:

Since it’s the relaxation of the problem of finding the maximum independent set, 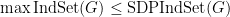 for any graph
for any graph  . And this relaxation has a nice property.
. And this relaxation has a nice property.
For every  , and for every graph
, and for every graph  , we have \begin{equation*} {\rm SDPIndSet}(G) \leq \frac 1p \cdot || pJ – A || \end{equation*} where
, we have \begin{equation*} {\rm SDPIndSet}(G) \leq \frac 1p \cdot || pJ – A || \end{equation*} where 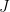 is the all-one matrix and
is the all-one matrix and  is the adjacency matrix of
is the adjacency matrix of  .
.
Proof: First we note that SDPIndSet is at most
is at most
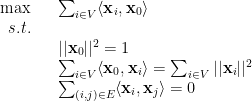
and this is equal to
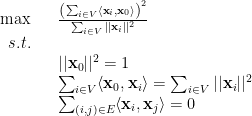
which is at most

because

Finally, the above optimization is equivalent to the following

which is at most the unconstrained problem


Recall from the previous section that we constructed 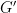 by removing edges from
by removing edges from  , which corresponds to removing constraints in our semidefinite programming problem, so
, which corresponds to removing constraints in our semidefinite programming problem, so  , which is by theorem 3 at most
, which is by theorem 3 at most  with high probability.
with high probability.
4. SDP relaxation of random k-SAT
From the previous section, we get an idea that we can use semidefinite programming to relax the problem directly and find a certificate of unsatisfiability for the relaxed problem.
Given a random  -SAT formula
-SAT formula  :
:

The satisfiability of  is equivalent of the satisfiability of the following equations:
is equivalent of the satisfiability of the following equations:
![\displaystyle \begin{array}{rcl} && x_i^2 = x_i \forall i \in [n] \\ && \sum_{i = 1}^m \left(1 - \prod_{j = 1}^k\left((-1)^{b_{i,j}}x_{\sigma_{i,j}} + b_{i,j}\right)\right) = m \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cbegin%7Barray%7D%7Brcl%7D++%26%26+x_i%5E2+%3D+x_i+%5Cforall+i+%5Cin+%5Bn%5D+%5C%5C+%26%26+%5Csum_%7Bi+%3D+1%7D%5Em+%5Cleft%281+-+%5Cprod_%7Bj+%3D+1%7D%5Ek%5Cleft%28%28-1%29%5E%7Bb_%7Bi%2Cj%7D%7Dx_%7B%5Csigma_%7Bi%2Cj%7D%7D+%2B+b_%7Bi%2Cj%7D%5Cright%29%5Cright%29+%3D+m+%5Cend%7Barray%7D+&bg=ffffff&fg=000000&s=0&c=20201002)
Notice that if we expand the polynomial on the left side, there are some of the monomials having degree higher than 2 which prevents us relaxing these equations to a semidefinite programming problem. In order to resolve this,  and
and 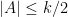 we introduce
we introduce  . Then we can relax all variables to be vectors, i.e.
. Then we can relax all variables to be vectors, i.e.
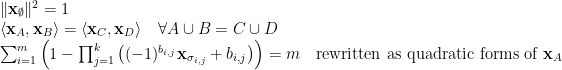
For example, if we have a 4-SAT clause

we can rewrite it as

For this relaxation, we have:
- If
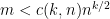 , the SDP associated with the formula is feasible with high probability, where
, the SDP associated with the formula is feasible with high probability, where 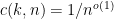 for every fixed
for every fixed  .
.
- If
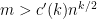 , the SDP associated with the formula is not feasible with high probability, where
, the SDP associated with the formula is not feasible with high probability, where  is a constant for every fixed even
is a constant for every fixed even  , and
, and  for every fixed odd
for every fixed odd  .
.

