A conjectural approaches to the Riemann hypothesis is to find a correspondence between the zeroes of the zeta function and the eigenvalues of a linear operator. This was first conceived by Hilbert and by Pólya in the 1910s. (See this correspondence with Odlyzko.) In the subsequent century, there have been a number of rigorous results relating the zeroes of zeta functions in other settings to eigenvalues of linear operators. There is also a connection between the distribution of known zeroes of the Riemann zeta function, as derived from explicit calculations, and the distribution of eigenvalues of the Gaussian unitary ensemble.
In a previous post we talked about the definition of the Ihara zeta function of a graph, and Ihara’s explicit formula for it, in terms of a determinant that is closely related to the characteristic polynomial of the adjacency matrix of the graph, so that the zeroes of the zeta function determine the eigenvalue of the graph. And if the zeta function of the graph satisfies a “Riemann hypothesis,” meaning that, after a change of variable, all zeroes and poles of the zeta function are  in absolute value, then the graph is Ramanujan. Conversely, if the graph is Ramnujan then its Ihara zeta function must satisfy the Riemann hypothesis.
in absolute value, then the graph is Ramanujan. Conversely, if the graph is Ramnujan then its Ihara zeta function must satisfy the Riemann hypothesis.
As I learned from notes by Pete Clark, the zeta functions of curves and varieties in finite fields also involve a determinant, and the “Riemann hypothesis” for such curves is a theorem (proved by Weil for curves and by Deligne for varieties), which says that (after an analogous change of variable) all zeroes and poles of the zeta function must be  in absolute value, where
in absolute value, where  is the size of the finite field. This means that one way to prove that a family of
is the size of the finite field. This means that one way to prove that a family of  -regular graphs is Ramanujan is to construct for each graph
-regular graphs is Ramanujan is to construct for each graph  in the family a variety
in the family a variety 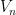 over
over  such that the determinant that comes up in the zeta function of
such that the determinant that comes up in the zeta function of  is the “same” (up to terms that don’t affect the roots, and to the fact that if
is the “same” (up to terms that don’t affect the roots, and to the fact that if  is a root for one characteristic polynomial, then
is a root for one characteristic polynomial, then 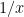 has to be a root for the other) as the determinant that comes up in the zeta function of the variety
has to be a root for the other) as the determinant that comes up in the zeta function of the variety 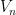 . Clark shows that one can constructs such families of varieties (in fact, curves are enough) for all the known algebraic constructions of Ramanujan graphs, and one can use families of varieties for which the corresponding determinant is well understood to give new constructions. For example, for every
. Clark shows that one can constructs such families of varieties (in fact, curves are enough) for all the known algebraic constructions of Ramanujan graphs, and one can use families of varieties for which the corresponding determinant is well understood to give new constructions. For example, for every  , if
, if  is the number of distinct prime divisors of
is the number of distinct prime divisors of  (which would be one if
(which would be one if  is a prime power) Clark gets a family of graphs with second eigenvalue
is a prime power) Clark gets a family of graphs with second eigenvalue 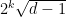 . (The notes call
. (The notes call  the number of distinct prime divisors of
the number of distinct prime divisors of  , but it must be a typo.)
, but it must be a typo.)
So spectral techniques underlie fundamental results in number theory and algebraic geometry, which then give us expander graphs. Sounds like something that we (theoretical computer scientists) should know more about.
The purpose of these notes is to explore a bit more the statements of these results, although we will not even begin to discuss their proofs.
One more reason why I find this material very interesting is that all the several applications of polynomials in computer science (to constructing error-correcting codes, secret sharing schemes,  -wise independent generators, expanders of polylogarithmic degree, giving the codes used in PCP constructions, self-reducibility of the permanent, proving combinatorial bounds via the polynomial method, and so on), always eventually rely on three things:
-wise independent generators, expanders of polylogarithmic degree, giving the codes used in PCP constructions, self-reducibility of the permanent, proving combinatorial bounds via the polynomial method, and so on), always eventually rely on three things:
This is enough to explain the remarkable pseudo-randomness of constructions that we get out of polynomials, and it is the set of principles that underlie much of what is below, except that we are going to restrict polynomials to the set of zeroes of another polynomial, instead of a line, and this is where things get much more complicated, and interesting.
Before getting started, however, I would like to work out a toy example (which is closely related to what goes on with the Ihara zeta function) showing how an expression that looks like the one defining zeta functions can be expressed as a characteristic polynomial of a linear operator, and how its roots (which are then the eigenvalues of the operator) help give bound to a counting problem, and how one can get such bounds directly from the trace of the operator.
If we have quantities  that we want to bound, then the “zeta function” of the sequence is
that we want to bound, then the “zeta function” of the sequence is
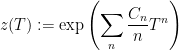
For example, and this will be discussed in more detail below, if  if a bivariate polynomial over
if a bivariate polynomial over  , we may be interested in the number
, we may be interested in the number 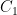 of solutions of the equation
of solutions of the equation  over
over  , as well as the number of solutions
, as well as the number of solutions  over the extension
over the extension 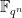 . In this case, the zeta function of the curve defined by
. In this case, the zeta function of the curve defined by 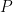 is precisely
is precisely
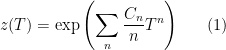
and Weil proved that 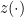 is a rational function, and that if
is a rational function, and that if  are the zeroes and poles of
are the zeroes and poles of  , that is, the roots of the numerator and the denominator, then they are all at most
, that is, the roots of the numerator and the denominator, then they are all at most  in absolute value, and one has
in absolute value, and one has
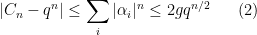
How does one get an approximate formula for  as in (2) from the zeroes of a function like (1), and what do determinants and traces have got to do with it?
as in (2) from the zeroes of a function like (1), and what do determinants and traces have got to do with it?
Here is our toy example: suppose that we have a graph  and that
and that  is the number of cycles of the graph of length
is the number of cycles of the graph of length 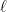 . Here by “cycle of length
. Here by “cycle of length 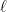 ” we mean a sequence
” we mean a sequence 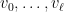 of vertices such that
of vertices such that  and, for
and, for 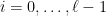 ,
, 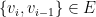 . So, for example, in a graph in which the vertices
. So, for example, in a graph in which the vertices 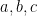 form a triangle,
form a triangle, 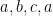 and
and  are two distinct cycles of length 3, and
are two distinct cycles of length 3, and 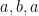 is a cycle of length 2.
is a cycle of length 2.
We could define the function
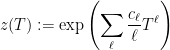
and hope that its zeroes have to do with the computation of  , and that
, and that  can be defined in terms of the characteristic polynomial.
can be defined in terms of the characteristic polynomial.
Indeed, we have (remember,  is a complex number, not a matrix):
is a complex number, not a matrix):
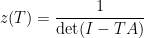
and, if  are the zeroes and poles of
are the zeroes and poles of  , then
, then
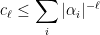
How did we get these bounds? Well, we cheated because we already knew that  , where
, where 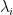 are the eigenvalues of
are the eigenvalues of  . This means that
. This means that
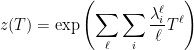
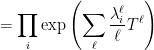

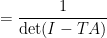
Where we used 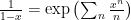 . Now we see that the poles of
. Now we see that the poles of  are precisely the inverses of the eigenvalues of
are precisely the inverses of the eigenvalues of  .
.
Now we are ready to look more closely at various zeta functions.
I would like to thank Ken Ribet and Jared Weinstein for the time they spent answering questions. Part of this post will follow, almost word for word, this post of Terry Tao. All the errors and misconceptions below, however, are my own original creation.
Continue reading →
, and then interpreting the above concepts and algorithms in graph-theoretic language. The most natural representation of a graph as a matrix is via the
adjacency matrix of a graph, and certain related matrices, such as the Laplacian and normalized Laplacian matrix will be our main focus. We can think of
-dimensional Boolean vectors as a representing a partition of the vertices, that is, a cut in the graph, and we can think of arbitrary vectors as fractional cuts. From this point of view, eigenvalues are the optima of continuous relaxations of certain cut problems, the corresponding eigenvectors are optimal solutions, and connections between spectrum and cut structures are given by rounding algorithms converting fractional solutions into integral ones. Flow problems are dual to cut problems, so one would expect linear algebraic techniques to be helpful to find flows in networks: this is the case, via the theory of electrical flows, which can be found as solutions to linear systems.
, where
is Laplacian of a graph, their applications to finding electrical flows, and the applications of electrical flows to solving the max flow problem.
