Suppose are mutually independent unbiased
random variables. Then we know everything about the distribution of
either by using the central limit theorem or by doing calculations by hand using binomial coefficients and Stirling’s approximation. In particular, we know that (1) takes the values with probability
each, and so with constant probability (1) is at most
.
The last statement can be proved from scratch using only pairwise independence. We compute
so that
It is also true that (1) is at least with constant probability, and this is trickier to prove.
First of all, note that a proof based on pairwise independence is not possible any more. If is a random row of an Hadamard matrix, then
with probability
, and
with probability
.
Happily, four-wise independence suffices.
Lemma 1 Suppose
are four-wise independent
random variables. Then
This is probably well known to a lot of people, but the only place where I have seen this result is a paper by Andreev et al. that I have mentioned before.
Here is a slightly simplified version of their argument. We compute
and
So we have (from here on is our simplified version)
and
Thus
Following the same proof, but replacing each “” with “
” and every “
” with “
”, we get the more general version
Lemma 2 Suppose
are four-wise independent
random variables and let
be any real numbers. Then
In particular,
A related version that was useful in our work on distinguishers for pseudorandom generators is
Corollary 3 Let
be a four-wise independent family of functions
and
be any real valued function. Then
To briefly show how this relates to our work on distinguishers, suppose is a length-increasing function, and that we want to construct a function
, computable by a circuit as small as possible, such that
Then this is equivalent to proving
and, if we set
then (2) is equivalent to
Now, fix a simple partition of
into
subsets each of size
, for example based on the value of the first
bits.
Fix an efficiently computable four-wise independent family of functions
. Then we have, for every set
in the partition
and if we sum over all sets in the partition we have
In particular, there is a function such that
To finish the argument, define the function such that
iff
, where
is the set that
belongs to. Then
-
depends only on the first
bits of the input, and so it can be computed by a circuit of size
- for every
we have
So, in conclusion
meaning that setting satisfies (3), and gives us a distinguisher obtaining advantage
and having circuit complexity
.

Hi Luca,
You are using/proving the Payley-Zygmund inequality, also popularly known as the “second moment method.”
Similar results have been obtained by Serge Vaudenay using his “decorrelation theory” [1] in the context of the design of secure block ciphers. More precisely, his paper [2] about iterated distinguishers shows that a decorrelation of order $2d$ is sufficient to resist an attack of order $d$. An open question is whether this is a necessary condition.
[1] S. Vaudenay, “Decorrelation: A Theory for Block Cipher Security”, J. Cryptology, 16(4), 249-286, 2003.
[2] S. Vaudenay, “Resistance against general iterated attacks”, Proceedings of Eurocrypt’99, pp. 255-271, LNCS 1592, Springer, 1999.
Hi Luca,
Lemma 1 was also proven by Bonnie Berger back in SODA ’91. See her paper, “The Fourth Moment Method”.
Yeah, what James said, with Wikipedia’s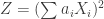 . Indeed, if the
. Indeed, if the 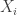 ‘s in Lemma 2 are any
‘s in Lemma 2 are any  -hypercontractive random variables, then so too is
-hypercontractive random variables, then so too is  ; then Paley-Zygmund gives the lower bound (with the RHS depending on
; then Paley-Zygmund gives the lower bound (with the RHS depending on  ).
).
Thanks, Jelani, and her calculations are much tighter, in Lemma 2 she has a factor of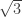 instead of 20 (Andreev, Clementi and Rolim had 96)
instead of 20 (Andreev, Clementi and Rolim had 96)
Hi Pascal, what is the similarity that you see? Vaudenay shows that if a family of permutations is close to k-wise independent under certain norms then certain classes of attackers have small advantage in distinguishing a function from the family from a truly random permutation. (And some of those conditions are necessary in order to upper bound the advantage of distinguishers from those classes.)
Here we have a completely arbitrary distribution over -bit strings that is far from uniform in total variation distance (for concreteness I have talked about the output of a length-increasing generator) and we show that, within a set S, a distinguisher sampled from a 4-wise independent family of functions has typically advantage about
-bit strings that is far from uniform in total variation distance (for concreteness I have talked about the output of a length-increasing generator) and we show that, within a set S, a distinguisher sampled from a 4-wise independent family of functions has typically advantage about  times the best possible advantage within the set S.
times the best possible advantage within the set S.
(So if we are willing to invest in a look-up table of size to know the sign of the distinguishing probability in each set of size
to know the sign of the distinguishing probability in each set of size 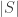 into which we partition
into which we partition  , we can get advantage
, we can get advantage 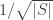 overall. This is not an iterated attack because there are no queries to make, it’s just a case analysis.)
overall. This is not an iterated attack because there are no queries to make, it’s just a case analysis.)
So here it’s the attacker, not the construction that is coming from a -wise independent distribution, and we are proving a lower bound, not an upper bound, on the distinguishing probability.
-wise independent distribution, and we are proving a lower bound, not an upper bound, on the distinguishing probability.
I had a question along similar lines on sum of -wise independent variables. Assume
-wise independent variables. Assume 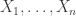 are
are  -wise independent
-wise independent  random variables. What can be said about the following expression :
random variables. What can be said about the following expression :
By Berry – Esseen theorem, if , then it is
, then it is 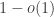 and the above discussion shows that
and the above discussion shows that 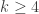 implies that it is bigger than a constant. But can we get a better bound if
implies that it is bigger than a constant. But can we get a better bound if  ?
?
Hi Anindya,
If the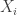 are k-wise independent for
are k-wise independent for 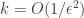 , then
, then
Note when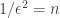 , this gives a lower bound of
, this gives a lower bound of 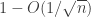 , which is what Berry-Esseen would tell you.
, which is what Berry-Esseen would tell you.
(*) follows from Section A.5 of http://web.mit.edu/minilek/www/papers/lp.pdf (last paragraph, which refers back to an earlier argument in the paper ^^;), though I regret that recovering (*) from what’s written there might take a bit of sorting through our notation, since the paper is really about something else. You can also get (*) from “Bounded Independence Fools Halfspaces” (Diakonikolas et al., FOCS ’09) with only a slightly larger k of .
.
What do we know anything about how tight (*) is, in Jelani’s previous comment?
I don’t understand: if the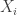 are mutually independent, then from the Berry-Esseen theorem we have that for every threshold
are mutually independent, then from the Berry-Esseen theorem we have that for every threshold 
where is a normal random variable with expectation zero and variance 1. But the probability that
is a normal random variable with expectation zero and variance 1. But the probability that 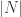 is more than
is more than  is not
is not 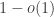 , it is a constant bounded away from 1 (and from zero).
, it is a constant bounded away from 1 (and from zero).
I think Luca is right though I intended to put instead of
instead of 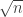 . In that case, Berry-Esseen does guarantee that the sum of
. In that case, Berry-Esseen does guarantee that the sum of 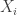 exceeds
exceeds  in absolute value with
in absolute value with 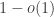 probability. However, a calculation like above does not give anything beyond a constant probability.
probability. However, a calculation like above does not give anything beyond a constant probability.
Jelani: Thanks for answering. I assume what you guys prove is that if , then the difference from the Normal distribution is at most $\epsilon$. That sounds great though I have not yet read your paper.
, then the difference from the Normal distribution is at most $\epsilon$. That sounds great though I have not yet read your paper.
What I should have actually said is, as long as the $X_i$ are $k$-wise independent for $k = \Omega(1/\epsilon^2)$ then
$$ \mathrm{Pr}[|\sum_i X_i| > \epsilon \sqrt{n}] \ge 1 – O(\epsilon) $$
I forgot to type that inner $\epsilon$ above. Sorry for the confusion.
In general, proving concentration bounds under bounded independence has been known for a while. What I believe was not known until recently, is that bounded independence also suffices for anti-concentration bounds. More generally, the following holds:
The Berry-Esseen version of the CLT also applies under bounded independence.
In particular, in Luca’s formulation, if the X_i’ s in the sum are \Omega(1/eps^2)-wise independent, then the distance between the CDF’s is at most 1/\sqrt{n} + eps. (**)
The degree of independence required for such a statement to hold is actually Omega(1/eps^2), i.e. the above bound is optimal up to constant factors.
As Jelani pointed out, (**) follows as a special case of a result by Gopalan, Jaiswal, Servedio, Viola and myself, but the bound there on the degree of independence required is slightly weaker (up to a log^2 factor).
See:
http://www.emis.de/journals/EJP-ECP/_ejpecp/ECP/viewarticle895c.html?id=1796&layout=abstract
In relation to this and possible behaviour when higher independence is assumed.
That had been incredibly imformative. I appreciate you all the material.